Question

2．如图1，已知正方形ABCD，点E、F、G、H分别在边AB、BC、CD、DA上，若EG⊥FH，则易证：EG=FH．
（1）如果把条件中的“正方形”改为“长方形”，并设AB=2，BC=3（如图2），试探究EG、FH之间有怎样的数量关系，并证明你的结论；
（2）如果把条件中的“EG⊥FH”改为“EG与FH的夹角为45°”，并假设正方形ABCD的边长为1，FH的长为$\frac{\sqrt{5}}{2}$（如图3），试求EG的长度．

Answer 1

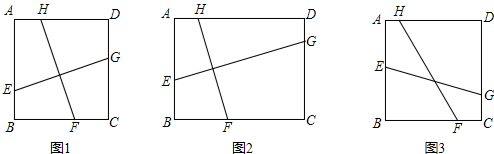
分析 （1）将全等三角形改成了相似三角形，通过相似三角形得出的对应线段成比例来得出EG：FH=3：2；
（2）按（1）的思路也要通过构建全等三角形来求解，可过点A作AM∥HF交BC于点M，过点A作AN∥EG交CD于点N，将△AND绕点A旋转到△APB，不难得出△APM和△ANM全等，那么可得出PM=MN，而MB的长可在直角三角形ABM中根据AB和AM（即HF的长）求出．如果设DN=x，那么NM=PM=BM+x，MC=BC-BM=1-BM，因此可在直角三角形MNC中用勾股定理求出DN的长，进而可在直角三角形AND中求出AN即EG的长．

解答 （1）结论：EG：FH=3：2
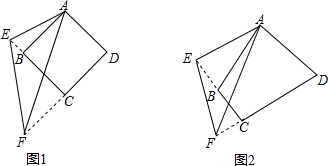
证明：过点A作AM∥HF交BC于点M，作AN∥EG交CD的延长线于点N，如图1：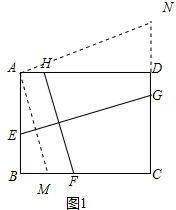

∴AM=HF，AN=EG，
∵长方形ABCD，
∴∠BAD=∠ADN=90°，
∵EG⊥FH，
∴∠NAM=90°，
∴∠BAM=∠DAN，
∴△ABM∽△ADN，
∴$\frac{AM}{AN}=\frac{AB}{AD}$，
∵AB=2BC=AD=3，
∴$\frac{EG}{FH}=\frac{3}{2}$；
（2）解：过点A作AM∥HF交BC于点M，过点A作AN∥EG交CD于点N，如图2：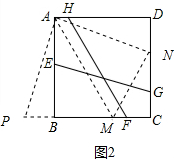

∵AB=1，AM=FH=$\frac{\sqrt{5}}{2}$，
∴在Rt△ABM中，BM=$\frac{1}{2}$将△AND绕点A旋转到△APB，
∵EG与FH的夹角为45°，
∴∠MAN=45°，
∴∠DAN+∠MAB=45
即∠PAM=∠MAN=45°，
从而△APM≌△ANM，
∴PM=NM，
设DN=x，则NC=1-x，NM=PM=$\frac{1}{2}$+x
在Rt△CMN中，（$\frac{1}{2}$+x）²=$\frac{1}{4}$+（1-x）²，
解得x=$\frac{1}{3}$，
∴EG=AN=$\sqrt{1-{x}^{2}}=\frac{\sqrt{10}}{3}$，
答：EG的长为$\frac{\sqrt{10}}{3}$．

点评 本题主要考查了正方形的性质、全等三角形的判定和性质、相似三角形的判定和性质、图形的旋转变换等知识．通过辅助线或图形的旋转将所求的线段与已知的线段构建到一对全等或相似的三角形中是本题的基本思路．