
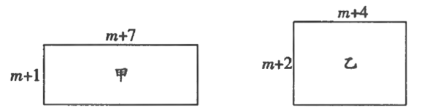
【题目】甲、乙两个长方形的边长如图所示(![]() 为正整数),其面积分别为
为正整数),其面积分别为![]() .
.
(1)填空:![]() (用含
(用含![]() 的代数式表示);
的代数式表示);
(2)若一个正方形的周长等于甲、乙两个长方形的周长之和.
①设该正方形的边长为![]() ,求
,求![]() 的值(用含
的值(用含![]() 的代数式表示);
的代数式表示);
②设该正方形的面积为![]() ,试探究:
,试探究: ![]() 与
与![]() 的差是否是常数?若是常数,求出这个常数,若不是常数,请说明理由,
的差是否是常数?若是常数,求出这个常数,若不是常数,请说明理由,
(3)若另一个正方形的边长为正整数![]() ,并且满足条件
,并且满足条件![]() 的
的![]() 有且只有4个,求
有且只有4个,求![]() 的值.
的值.
【答案】(1)2m-1;(2)①x的值为:2m+7;②![]() 与
与![]() 的差是常数,这个常数是19;(3)m的值为3.
的差是常数,这个常数是19;(3)m的值为3.
【解析】
(1)根据长方形的面积公式分别求出![]() ,再作差即可得出答案;
,再作差即可得出答案;
(2)①根据长方形的周长公式求出甲乙两个长方形的周长,再根据正方形的周长公式求出x,即可得出答案;②利用①求出的x,求出正方形的面积![]() ,代入
,代入![]() 化简即可得出答案;
化简即可得出答案;
(3) 根据题意求出![]() 的取值范围,即得到2m-1的取值范围,根据取值范围求出m的值,再根据m是正整数这一条件得出m的值.
的取值范围,即得到2m-1的取值范围,根据取值范围求出m的值,再根据m是正整数这一条件得出m的值.
解:(1)由题意可得:![]()
![]()
∴![]()
(2)①∵正方形的周长等于甲、乙两个长方形的周长之和
∴正方形的周长=2(m+7+m+1)+2(m+4+m+2)=8m+28
又正方形的边长为![]()
∴4x=8m+28
解得:x=2m+7
∴x的值为:2m+7.
②由①可知,![]()
∴![]()
故![]() 与
与![]() 的差是常数,这个常数是19.
的差是常数,这个常数是19.
(3)∵![]() 的
的![]() 有且只有4个
有且只有4个
∴![]()
即4<2m-1≤5
解得:![]()
又m为正整数
∴m=3
故m的值为3.


科目:初中数学 来源: 题型:
【题目】某大学计划为新生配备如图1所示的折叠凳.图2是折叠凳撑开后的侧面示意图(木条等材料宽度忽略不计),其中凳腿AB和CD的长相等,O是它们的中点.为了使折叠凳坐着舒适,厂家将撑开后的折叠凳宽度AD设计为30 cm,由以上信息能求出CB的长度吗?请你说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为6cm的正方形ABCD折叠,使点D落在AB边的中点E处,折痕为FH,点C落在Q处,EQ与BC交于点G,则△EBG的周长是 cm.
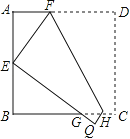
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中,![]() 为
为![]() 的中点,过点
的中点,过点![]() 的直线分别与
的直线分别与![]() 、
、![]() 交于点
交于点![]() 、
、![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() .若
.若![]() ,
,![]() ,则下列结论:①
,则下列结论:①![]() ;②
;②![]() ;③四边形
;③四边形![]() 是菱形;④
是菱形;④![]() .其中正确结论的个数是( )
.其中正确结论的个数是( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知有理数a,b在数轴上的位置如图所示.
(1)在数轴上标出﹣a,﹣b的位置,并比较a,b,﹣a,﹣b的大小:
(2)化简|a+b|+|a﹣b|.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
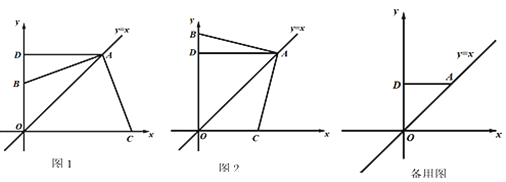
【题目】如图,点A为平面直角坐标系第一象限内一点,直线y=x过点A,过点A作AD⊥y轴于点D,点B是y轴正半轴上一动点,连接AB,过点A作AC⊥AB交x轴于点C.
(1)如图,当点B在线段OD上时,求证:AB=AC;
(2)①如图,当点B在OD延长线上,且点C在x轴正半轴上, OA、OB、OC之间的数量关系为________(不用说明理由);
②当点B在OD延长线上,且点C在x轴负半轴上,写出OA、OB、OC之间的数量关系,并说明原因.
(3)直线BC分别与直线AD、直线y=x交于点E、F,若BE=5,CF=12,直接写出AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年新型冠状病毒肺炎疫情肆虐,红星社区为了提高社区居民的身体素质,鼓励居民在家锻炼,特采购了一批跳绳免费发放,已知2根幸福牌跳绳和1根平安牌跳绳共需31元,2根平安牌跳绳和3根幸福牌跳绳共需54元.
(1)求幸福牌跳绳和平安牌跳绳的单价;
(2)已知该社区需要采购两种品牌的跳绳共60根,且平安牌跳绳的数量不少于幸福牌跳绳数量的2倍,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
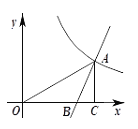
【题目】如图,直线y1=2x-3与双曲线![]() 在第一象限交于点A,与x轴交于点B,过点A作AC⊥x轴,垂足为C,已知∠BAC=∠AOC.
在第一象限交于点A,与x轴交于点B,过点A作AC⊥x轴,垂足为C,已知∠BAC=∠AOC.
(1)求A,B两点的坐标及k的值;
(2)请直接写出当y2>y1>0时x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com