
 某景区修建一栋复古建筑,其窗户设计如图所示.圆O的圆心与矩形ABCD对角线的交点重合,且圆与矩形上下两边相切(E为上切点),与左右两边相交(F,G为其中两个交点),图中阴影部分为不透光区域,其余部分为透光区域.已知圆的半径为1m,根据设计要求,若∠EOF=45°,则此窗户的透光率(透光区域与矩形窗面的面积的比值)为$\frac{(π+2)\sqrt{2}}{8}$.
某景区修建一栋复古建筑,其窗户设计如图所示.圆O的圆心与矩形ABCD对角线的交点重合,且圆与矩形上下两边相切(E为上切点),与左右两边相交(F,G为其中两个交点),图中阴影部分为不透光区域,其余部分为透光区域.已知圆的半径为1m,根据设计要求,若∠EOF=45°,则此窗户的透光率(透光区域与矩形窗面的面积的比值)为$\frac{(π+2)\sqrt{2}}{8}$. 分析 把透光部分看作是两个直角三角形与四个45°的扇形的组合体,其和就是透光的面积,再计算矩形的面积,相比可得结果.
解答 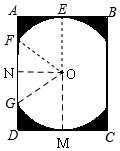 解:设⊙O与矩形ABCD的另一个交点为M,
解:设⊙O与矩形ABCD的另一个交点为M,
连接OM、OG,则M、O、E共线,
由题意得:∠MOG=∠EOF=45°,
∴∠FOG=90°,且OF=OG=1,
∴S透明区域=$\frac{180π×{1}^{2}}{360}$+2×$\frac{1}{2}$×1×1=$\frac{π}{2}$+1,
过O作ON⊥AD于N,
∴ON=$\frac{1}{2}$FG=$\frac{1}{2}$$\sqrt{2}$,
∴AB=2ON=2×$\frac{1}{2}\sqrt{2}$=$\sqrt{2}$,
∴S矩形=2×$\sqrt{2}$=2$\sqrt{2}$,
∴$\frac{{S}_{透光区域}}{{S}_{矩形}}$=$\frac{\frac{π}{2}+1}{2\sqrt{2}}$=$\frac{\sqrt{2}(π+2)}{8}$.
故答案为:$\frac{(π+2)\sqrt{2}}{8}$.
点评 本题考查了矩形的性质、扇形的面积、直角三角形的面积,将透光部分化分为几个熟知图形的面积是关键.


科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,若BD=2AD,则( )
如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,若BD=2AD,则( )| A. | $\frac{AD}{AB}=\frac{1}{2}$ | B. | $\frac{AE}{EC}=\frac{1}{2}$ | C. | $\frac{AD}{EC}=\frac{1}{2}$ | D. | $\frac{DE}{BC}=\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 人数(人) | 1 | 3 | 4 | 1 |
| 分数(分) | 80 | 85 | 90 | 95 |
| A. | 90,90 | B. | 90,85 | C. | 90,87.5 | D. | 85,85 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
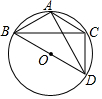 如图,等腰△ABC内接于⊙O,已知AB=AC,∠ABC=30°,BD是⊙O的直径,如果CD=$\frac{4\sqrt{3}}{3}$,则AD=4.
如图,等腰△ABC内接于⊙O,已知AB=AC,∠ABC=30°,BD是⊙O的直径,如果CD=$\frac{4\sqrt{3}}{3}$,则AD=4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
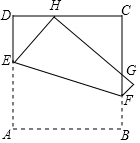 如图,将正方形ABCD折叠,使顶点A与CD边上的一点H重合(H不与端点C,D重合),折痕交AD于点E,交BC于点F,边AB折叠后与边BC交于点G.设正方形ABCD的周长为m,△CHG的周长为n,则$\frac{n}{m}$的值为( )
如图,将正方形ABCD折叠,使顶点A与CD边上的一点H重合(H不与端点C,D重合),折痕交AD于点E,交BC于点F,边AB折叠后与边BC交于点G.设正方形ABCD的周长为m,△CHG的周长为n,则$\frac{n}{m}$的值为( )| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{1}{2}$ | ||
| C. | $\frac{\sqrt{5}-1}{2}$ | D. | 随H点位置的变化而变化 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com