
【题目】.如图 1,B、D 分别是 x 轴和 y 轴的正半轴上的点,AD∥x 轴,AB∥y 轴(AD>AB),点 P 从 C 点出发,以 3cm/s 的速度沿 CDAB 匀速运动,运动到 B 点时终止;点 Q 从 B 点出发,以 2cm/s 的速度,沿 BCD 匀速运动,运动到 D 点时终止.P、Q 两点同时出发, 设运动的时间为 t(s),△PCQ 的面积为 S(cm2),S 与 t 之间的函数关系由图 2 中的曲线段 OE,线段 EF、FG 表示.
(1)求 AD 点的坐标;

(2)求图2中线段FG的函数关系式;
(3)是否存在这样的时间 t,使得△PCQ 为等腰三角形?若存在,直接写出 t 的值;若不存在, 请说明理由.
【答案】(1) D(0,3), A(6,3);(2) ![]() ;(3)
;(3)![]() ,
,![]() ,
,![]()
【解析】
(1)由图象可知CD=3×1=3,设AD=BC=a,根据点Q到达点C时,点P到达点A,列出方程即可求出a.
(2)当点Q在CD上,点P在AB上时,对应的函数图象是线段FG,由此即可解决问题.
(3)分三种情形讨论:①Q在BC上,P在CD上时,列出方程即可;
②Q在BC上,P在AD上时,由CP=CQ得6﹣2t![]() ,整理得5t2+6t﹣18=0解方程即可;
,整理得5t2+6t﹣18=0解方程即可;
由PQ=CQ得![]() 6﹣2t,整理得7t2﹣22t+18=0,△<0,无解.当PC=PQ得6﹣2t=2(3t﹣3),解得t
6﹣2t,整理得7t2﹣22t+18=0,△<0,无解.当PC=PQ得6﹣2t=2(3t﹣3),解得t![]() ;
;
③Q在CD上,P在AB上时,由CP=PQ列出方程即可.
(1)设AD=BC=a,由图象可知CD=AB=3,点Q到达点C时,点P到达点A,否则P、Q继续运动时,S与t的函数图象不是直线,∴![]() ,∴a=6,∴点A坐标(6,3),点D坐标(0,3).
,∴a=6,∴点A坐标(6,3),点D坐标(0,3).
(2)当点Q在CD上,点P在AB上时,对应的函数图象是线段FG,∴S![]() CQ6=3CQ=3(2t﹣6)=6t﹣18.
CQ6=3CQ=3(2t﹣6)=6t﹣18.
(3)分三种情况讨论:
①Q在BC上,P在CD上时,由CP=CQ得6﹣2t=3t,解得:t![]() (不合题意舍弃,
(不合题意舍弃,![]() 1);
1);
②Q在BC上,P在AD上时,由CP=CQ得:6﹣2t![]() ,整理得5t2+6t﹣18=0,t
,整理得5t2+6t﹣18=0,t![]() 或
或![]() (舍弃).
(舍弃).
由PQ=CQ,如图1.

作PK⊥OB于K,则DP=OK=3t﹣3,KQ=6﹣2t﹣(3t﹣3)=9﹣5t,∴PQ![]() ,∴
,∴![]() 6﹣2t,整理得7t2﹣22t+18=0,△<0,无解.
6﹣2t,整理得7t2﹣22t+18=0,△<0,无解.
当PC=PQ.如图2.
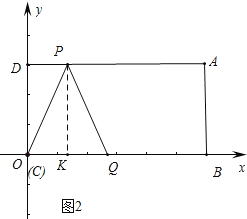
作PK⊥OB于K,则OK=KQ=DP,∴OQ=2DP,∴6﹣2t=2(3t﹣3),解得t![]() ;
;
③Q在CD上,P在AB上时,由CP=PQ,如图3.
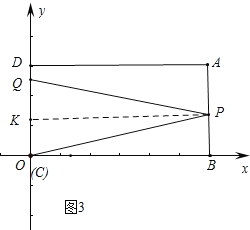
作PK⊥OD于K,则KQ=OK=PB,∴2PB=OQ,∴2(12﹣3t)=2t﹣6,解得:t![]() .
.
综上所述t![]() s或
s或![]() s或
s或![]() s时,△PCQ为等腰三角形.
s时,△PCQ为等腰三角形.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:
【题目】如图,有一形状为直角三角形的空地ABC,![]() ,
,![]() ,
,![]() ,现要作一条垂直于斜边AB的小道
,现要作一条垂直于斜边AB的小道![]() 点E在斜边上,点F在直角边上
点E在斜边上,点F在直角边上![]() 设
设![]() ,
,![]() 的面积为y.
的面积为y.
![]() 求y与x的函数关系式
求y与x的函数关系式![]() 写出自变量x的取值范围
写出自变量x的取值范围![]() ;
;
![]() 当x为何值时y有最大值?并求出最大值.
当x为何值时y有最大值?并求出最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】西瓜经营户以2元/千克的价格购进一批小型西瓜,以3元/千克的价格出售,每天可售出200千克.为了促销,该经营户决定降价销售.经调查发现,这种小型西瓜每降价0.1元/千克,每天可多售出40千克.另外,每天的房租等固定成本共24元,为了减少库存,该经营户要想每天盈利200元,应将每千克小型西瓜的售价降低( )元.
A.0.2或0.3
B.0.4
C.0.3
D.0.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2-(a+b)x+ab-1=0,x1、x2是此方程的两个实数根,现给出三个结论:①x1≠x2;②x1x2<ab;③![]() +
+![]() <a2+b2.则正确结论的序号是______.(填上你认为正确的所有序号)
<a2+b2.则正确结论的序号是______.(填上你认为正确的所有序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】央视热播节目“朗读者”激发了学生的阅读兴趣.某校为满足学生的阅读需求,欲购进一批学生喜欢的图书,学校组织学生会成员随机抽取部分学生进行问卷调查,被调查学生须从“文史类、社科类、小说类、生活类”中选择自己喜欢的一类,根据调查结果绘制了统计图(未完成),请根据图中信息,解答下列问题:
(1)此次共调查了 名学生;
(2)将条形统计图补充完整;
(3)图2中“小说类”所在扇形的圆心角为 度;
(4)若该校共有学生2500人,估计该校喜欢“社科类”书籍的学生人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了测量白塔的高度AB,在D处用高为1.5米的测角仪 CD,测得塔顶A的仰角为42°,再向白塔方向前进12米,又测得白塔的顶端A的仰角为61°,求白塔的高度AB.(参考数据sin42°≈0.67,tan42°≈0.90,sin61°≈0.87,tan61°≈1.80,结果保留整数)
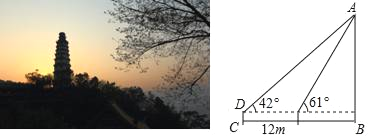
查看答案和解析>>
科目:初中数学 来源: 题型:
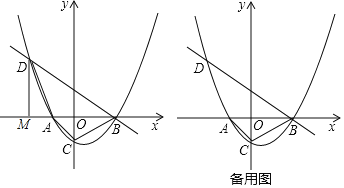
【题目】如图,已知抛物线![]() (k为常数,且
(k为常数,且![]() )与x轴从左至右依次交于A,B两点,与y轴交于点C过点B的直线
)与x轴从左至右依次交于A,B两点,与y轴交于点C过点B的直线![]() 与抛物线的另一交点为D.
与抛物线的另一交点为D.
![]() 若点D的横坐标为
若点D的横坐标为![]() ,求抛物线的函数表达式;
,求抛物线的函数表达式;
![]() 过D点向x轴作垂线,垂足为点M,连结AD,若
过D点向x轴作垂线,垂足为点M,连结AD,若![]() ,求点D的坐标;
,求点D的坐标;
![]() 若在第一象限的抛物线上有一点P,使得以点A,B,P为顶点的三角形与
若在第一象限的抛物线上有一点P,使得以点A,B,P为顶点的三角形与![]() 相似,请直接写出
相似,请直接写出![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com