
 如图,?ABCD中,O为BC边上一点,OD平分∠ADC,以O为圆心,OC为半径画圆,交OD于点E,若AB=6,?ABCD的面积是42$\sqrt{3}$,$\widehat{EC}$=π,请判断直线AB与⊙O的位置关系,并说明理由.
如图,?ABCD中,O为BC边上一点,OD平分∠ADC,以O为圆心,OC为半径画圆,交OD于点E,若AB=6,?ABCD的面积是42$\sqrt{3}$,$\widehat{EC}$=π,请判断直线AB与⊙O的位置关系,并说明理由. 分析 首先利用弧长公式求得圆心角∠COE的度数,进一步得到∠B=60°,作AM⊥BC于M,解直角三角形得到AM,根据三角形的面积公式即可求得BC的长,得到OB的长,作ON⊥AB于N,解直角三角形求得ON的长,然后与半径的长度比较大小即可.
解答 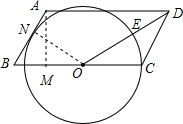 解:如图,∵四边形ABCD是平行四边形,
解:如图,∵四边形ABCD是平行四边形,
∴DC=AB=6,AD∥BC,∠B=∠ADC,
∴∠COD=∠ADO,
∵∠ADO=∠CDO,
∴∠COD=∠CDO,
∴OC=DC=6,
∴⊙O的半径为6,
设∠EOC为n°,则有π=$\frac{6nπ}{180}$.
n=30°.
∴∠ADC=60°,
∴∠B=60°,
作AM⊥BC于M,
∴AM=$\frac{\sqrt{3}}{2}$AB=3$\sqrt{3}$,
∵?ABCD的面积是42$\sqrt{3}$,
∴BC•AM=42$\sqrt{3}$,
∴BC=14,
∴OB=BC-OC=14-6=8,
作ON⊥AB于N,
∴ON=$\frac{\sqrt{3}}{2}$OB=4$\sqrt{3}$>6,
∴直线AB与⊙O相离.
点评 本题考查的是直线与圆的位置关系,解决此类问题可通过比较圆心到直线距离d与圆半径大小关系完成判定.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
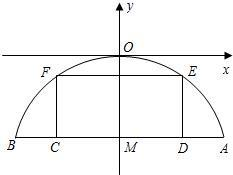 有一座抛物线型拱桥,其水面宽AB为18米,拱顶O离水面AB的距离OM为9米,货船在水面上的部分的横断面是矩形CDEF,如图建立平面直角坐标系.
有一座抛物线型拱桥,其水面宽AB为18米,拱顶O离水面AB的距离OM为9米,货船在水面上的部分的横断面是矩形CDEF,如图建立平面直角坐标系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2}{a}$ | B. | a-2 | C. | $\frac{a-2}{a}$ | D. | $\frac{a-4}{{a}^{2}+2a}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com