∠OEP=∠ODP或∠OEP+∠ODP=180°
分析:数量关系是∠OEP=∠ODP或∠OEP+∠ODP=180°,理由是以O为圆心,以OD为半径作弧,交OB于E
2,连接PE
2,根据SAS证△E
2OP≌△DOP,推出E
2P=PD,得出此时点E
2符合条件,此时∠OE
2P=∠ODP;以P为圆心,以PD为半径作弧,交OB于另一点E
1,连接PE
1,根据等腰三角形性质推出∠PE
2E
1=∠PE
1E
2,求出∠OE
1P+∠ODP=180°即可.
解答:

解:∠OEP=∠ODP或∠OEP+∠ODP=180°,
理由是:以O为圆心,以OD为半径作弧,交OB于E
2,连接PE
2,
∵在△E
2OP和△DOP中
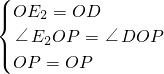
,
∴△E
2OP≌△DOP(SAS),
∴E
2P=PD,
即此时点E
2符合条件,此时∠OE
2P=∠ODP;
以P为圆心,以PD为半径作弧,交OB于另一点E
1,连接PE
1,
则此点E
1也符合条件PD=PE
1,
∵PE
2=PE
1=PD,
∴∠PE
2E
1=∠PE
1E
2,
∵∠OE
1P+∠E
2E
1P=180°,
∵∠OE
2P=∠ODP,
∴∠OE
1P+∠ODP=180°,
∴∠OEP与∠ODP所有可能的数量关系是:∠OEP=∠ODP或∠OEP+∠ODP=180°,
故答案为:∠OEP=∠ODP或∠OEP+∠ODP=180°.
点评:本题考查了全等三角形的性质和判定,等腰三角形的性质和判定等知识点,主要考查学生的猜想能力和分析问题和解决问题的能力,题目具有一定的代表性,是一道比较好的题目.

 如图,已知点P为∠AOB的角平分线上的一点,点D在边OA上.爱动脑筋的小刚经过仔细观察后,进行如下操作:在边OB上取一点E,使得PE=PD,这时他发现∠OEP与∠ODP之间有一定的相等关系,请你写出∠OEP与∠ODP所有可能的数量关系________.
如图,已知点P为∠AOB的角平分线上的一点,点D在边OA上.爱动脑筋的小刚经过仔细观察后,进行如下操作:在边OB上取一点E,使得PE=PD,这时他发现∠OEP与∠ODP之间有一定的相等关系,请你写出∠OEP与∠ODP所有可能的数量关系________. 解:∠OEP=∠ODP或∠OEP+∠ODP=180°,
解:∠OEP=∠ODP或∠OEP+∠ODP=180°,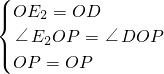 ,
,

 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案 如图,已知点C为线段AE上一点,AE=8cm,△ABC和△CDE为AE同侧的两个等边三角形,连接BE交CD于N,连接AD交BC于M,连接MN.
如图,已知点C为线段AE上一点,AE=8cm,△ABC和△CDE为AE同侧的两个等边三角形,连接BE交CD于N,连接AD交BC于M,连接MN.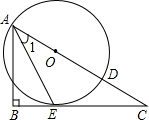 (2012•玉林)如图,已知点O为Rt△ABC斜边AC上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点E,与AC相交于点D,连接AE.
(2012•玉林)如图,已知点O为Rt△ABC斜边AC上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点E,与AC相交于点D,连接AE. 如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设
如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设 如图,已知点D为等腰直角△ABC内一点,AC=BC,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.若DE=acm,BD=bcm(a>b),则CD=
如图,已知点D为等腰直角△ABC内一点,AC=BC,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.若DE=acm,BD=bcm(a>b),则CD=