
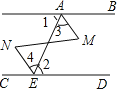
【题目】如图,直线AB,CD被直线AE所截,直线AM,EN被MN所截.请你从以下三个条件:①AB∥CD;②AM∥EN;③∠BAM=∠CEN中选出两个作为已知条件,另一个作为结论,得出一个正确的命题.
(1)请按照:“∵ , ;∴ ”的形式,写出所有正确的命题;
(2)在(1)所写的命题中选择一个加以证明,写出推理过程.
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:
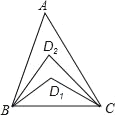
【题目】如图,在△ABC中,∠A=20°,∠ABC与∠ACB的角平分线交于D1,∠ABD1与∠ACD1的角平分线交于点D2,依此类推,∠ABD4与∠ACD4的角平分线交于点D5,则∠BD5C的度数是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2-6x+a-2=0.
(1)如果该方程有实数根,求实数a的取值范围;
(2)如果该方程有两个相等的实数根,求出这两个根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连接AC,过点D作DE⊥AC于E.
(1)求证:AB=AC;
(2)求证:DE为⊙O的切线.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,F为弦AC的中点,连接OF并延长交![]() 于点D,过点D作⊙O的切线,交BA的延长线于点E.
于点D,过点D作⊙O的切线,交BA的延长线于点E.
(1)求证:AC∥DE;
(2)连接CD,若OA=AE=1,求四边形ACDE面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明骑单车上学,当他骑了一段路时,想起要买某本书,于是又折回到刚经过的某书店,买到书后继续去学校,以下是他本次上学所用的时间与路程的关系示意图,根据图中提供的信息回答下列问题:
(1)小明家到学校的路程是______米;
(2)小明在书店停留了______分钟;
(3)本次上学途中,小明一共行驶了_____米,一共用了_______分钟;
(4)在整个上学的途中________(哪个时间段)小明骑车速度最快,最快的速度是____米/分.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行加价收费,为更好地做决策,自来水公司随机抽取部分用户的用水量数据,并绘制了如图不完整的统计图(每组数据包括最大值但不包括最小值),请你根据统计图解决下列问题:
(1)此次抽样调查的样本容量是
(2)补全左侧统计图,并求扇形统计图中“25吨~30吨”部分的圆心角度数.
(3)如果自来水公司将基本用水量定为每户25吨,那么该地区6万用户中约有多少用户的用水全部享受基本价格?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:线段![]()
求作:菱形![]() ,使得
,使得![]() 且
且![]() .
.
以下是小丁同学的作法:
①作线段![]() ;
;
②分别以点![]() ,
,![]() 为圆心,线段
为圆心,线段![]() 的长为半径作弧,两弧交于点
的长为半径作弧,两弧交于点![]() ;
;
③再分别以点![]() ,
,![]() 为圆心,线段
为圆心,线段![]() 的长为半径作弧,两弧交于点
的长为半径作弧,两弧交于点![]() ;
;
④连接![]() ,
,![]() ,
,![]() .
.
则四边形![]() 即为所求作的菱形.(如图)
即为所求作的菱形.(如图)
老师说小丁同学的作图正确.则小丁同学的作图依据是:_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com