
【题目】如图,在![]() 中,过对角线
中,过对角线![]() 上一点
上一点![]() 作
作![]() ,
,![]() ,且
,且![]() ,
,![]() ,则
,则![]() ( )
( )

A. 3 B. 4 C. 5 D. 6
【答案】B
【解析】
由EF∥BC,GH∥AB可知四边形HPFD、BEPG、AEPH、CFPG为平行四边形,所以S△PEB=S△BGP,S△PHD=S△DFP,S△ABD=S△CDB,根据S△ABD-S△PEB-S△PHD=S△CDB-S△BGP-S△DFP,即可证明S四边形AEPH=S四边形PFCG.根据CG=2BG,S△BPG=1即可求出S四边形AEPH.
∵EF∥BC,GH∥AB,
∴四边形HPFD、BEPG、AEPH、CFPG为平行四边形,
∴S△PEB=S△BGP,
同理可得S△PHD=S△DFP,S△ABD=S△CDB,
∴S△ABD-S△BPE -S△PHD=S△CDB-S△BGP-S△DFP,
即S四边形AEPH=S四边形PFCG.
∵CG=2BG,S△BPG=1,
∴S四边形AEPH=S四边形PFCG=4×1=4;
故选B.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,每个小正方形的边长为1,点A的坐标为(-3,2).请按要求分别完成下列各小题:
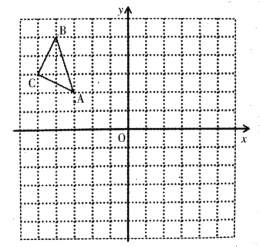
(1)把△ABC向下平移4个单位得到△A1B1C1,画出△A1B1C1,点A1的坐标是___.
(2)画出△ABC关于y轴对称的△A2B2C2,则点C2的坐标是 ;
(3)△ABC的面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,点E为边AB上任意一点,点D在边CB的延长线上,且ED=EC.

(1)当点E为AB的中点时(如图1),则有AE DB(填“>”“<”或“=”);
(2)猜想AE与DB的数量关系,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是甲、乙两家运输公司规定每位旅客携带行李的费用与所带行李质量之间的关系图.
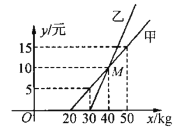
(1)由图可知,行李质量只要不超过______kg,甲公司就可免费携带,如果超过了规定的质量,则每超过1 kg要付运费_______元;
(2)若设旅客携带的行李质量为x(kg),所付的行李费是y(元),请分别写出y甲与y乙(元)随x(kg)之间变化的关系式;
(3)若你准备携带45 kg的行李出行,在甲、乙两家公司中你会选择哪一家?应付行李费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是菱形
是菱形![]() 的对角线
的对角线![]() 、
、![]() 的交点,
的交点,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点.下列结论:①
的中点.下列结论:①![]() ;②四边形
;②四边形![]() 也是菱形;③四边形
也是菱形;③四边形![]() 的面积为
的面积为![]() ;④
;④![]() ;⑤
;⑤![]() 是轴对称图形.其中正确的结论有( )
是轴对称图形.其中正确的结论有( )

A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校要开展校园文化艺术节活动,为了合理编排节目,对学生最喜爱的歌曲、舞蹈、小品、相声四类节目进行了一次抽样调查(每名学生必须选择且只能选择一类),并将调查结果绘制成如下不完整的统计图.
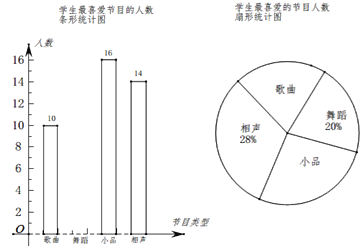
请你根据图中信息,回答下列问题:
(1)求本次调查的学生人数,并补全条形统计图;
(2)在扇形统计图中,求“歌曲”所在扇形的圆心角的度数;
(3)若该学校共有学生2000人,请问该学校大约有多少同学最喜爱“小品”节目?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
问题情境:在数学活动课上,老师出示了这样一个问题:如图1,在矩形ABCD中,AD=2AB,E是AB延长线上一点,且BE=AB,连接DE,交BC于点M,以DE为一边在DE的左下方作正方形DEFG,连接AM.试判断线段AM与DE的位置关系.
探究展示:勤奋小组发现,AM垂直平分DE,并展示了如下的证明方法:
证明:∵BE=AB,∴AE=2AB.
∵AD=2AB,∴AD=AE.
∵四边形ABCD是矩形,∴AD∥BC.
∴![]() .(依据1)
.(依据1)
∵BE=AB,∴![]() .∴EM=DM.
.∴EM=DM.
即AM是△ADE的DE边上的中线,
又∵AD=AE,∴AM⊥DE.(依据2)
∴AM垂直平分DE.
反思交流:
(1)①上述证明过程中的“依据1”“依据2”分别是指什么?
②试判断图1中的点A是否在线段GF的垂直平分线上,请直接回答,不必证明;
(2)创新小组受到勤奋小组的启发,继续进行探究,如图2,连接CE,以CE为一边在CE的左下方作正方形CEFG,发现点G在线段BC的垂直平分线上,请你给出证明;
探索发现:
(3)如图3,连接CE,以CE为一边在CE的右上方作正方形CEFG,可以发现点C,点B都在线段AE的垂直平分线上,除此之外,请观察矩形ABCD和正方形CEFG的顶点与边,你还能发现哪个顶点在哪条边的垂直平分线上,请写出一个你发现的结论,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC为等边三角形,点D为直线BC上一动点(点D不与点B,点C重合).以AD为边作等边三角形ADE,连接CE.
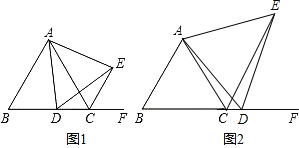
(1)如图1,当点D在边BC上时.求证:△ABD≌△ACE;
(2)如图2,当点D在边BC的延长线上时,其他条件不变,请写出BC,DC,CE之间存在的数量关系,并写出证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
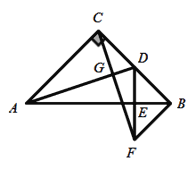
【题目】如图,在等腰![]() 中,
中,![]() ,D为BC的中点,过点C作
,D为BC的中点,过点C作![]() 于点G,过点B作
于点G,过点B作![]() 于点B,交CG的延长线于点F,连接DF交AB于点E.
于点B,交CG的延长线于点F,连接DF交AB于点E.
(1)求证:![]() ;
;
(2)求证:AB垂直平分DF;
(3)连接AF,试判断![]() 的形状,并说明理由.
的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com