
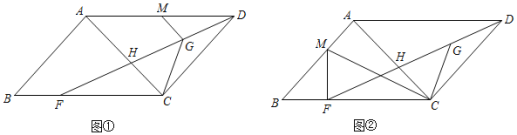
【题目】如图,ABCD中,DF平分∠ADC交AC于点H,G为DH的中点.
(1)如图①,若M为AD的中点,AB⊥AC,AC=9,CF=8,CG=2![]() ,求GM;
,求GM;
(2)如图②,M为线段AB上一点,连接MF,满足∠MCD=∠BCG,∠MFB=∠BAC.求证:MC=2CG.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)先根据平行四边形的性质和平行线的性质得出∠BAC=∠ACD=90,进而得出HD=![]() ,然后根据角平分线的性质和等腰三角形的性质得出CD=CF=8,然后由勾股定理求出CH的长度,从而求出AH的长度,最后利用三角形中位线的性质即可得出MG的长度;
,然后根据角平分线的性质和等腰三角形的性质得出CD=CF=8,然后由勾股定理求出CH的长度,从而求出AH的长度,最后利用三角形中位线的性质即可得出MG的长度;
(2)过点D作DN∥AC,交CG的延长线于点N,首先利用AAS证明△CGH≌△NGD得出GC=GN,从而有CN=2CG,然后通过平行四边形的性质和平行线的性质得出∠MFC=∠NDC,∠FCM=∠DCN,再加上CF=CD利用ASA即可证△MFC≌△NDC,从而得出CM=CN,即可证明CM=2CG.
(1)∵四边形ABCD是平行四边形,
![]() ,
,
∵AB⊥AC,
∴∠BAC=∠ACD=90°,
∵G为DH的中点,
∴CG=HG=GD,
∵CG=![]() ,
,
∴HD=![]() ,
,
∵DF平分∠ADC,
∴∠DFC=∠ADF=∠CDF,
∴CF=CD,
∵CF=8,
∴CD=8,
在Rt△HCD中,HC=![]() ,
,
∵AC=9,
∴AH=5,
∵M为AD的中点,G为DH的中点,
∴MG=![]() AH=
AH=![]() ;
;
(2)如图②,过点D作DN∥AC,交CG的延长线于点N,
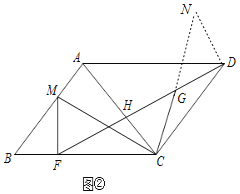
∵DN∥AC,
∴∠N=∠ACN,∠DAC=∠ADN,
∵G为DH的中点,
∴DG=HG,且∠N=∠ACG,∠CGH=∠DGN,
∴△CGH≌△NGD(AAS)
∴GC=GN,
∴CN=2CG,
∵∠MCD=∠BCG,
∴∠FCM=∠DCN,
∵四边形ABCD是平行四边形,
∴∠B=∠ADC,AD∥BC,
∴∠DAC=∠ACB=∠ADN,
∵∠MFB=∠BAC,∠B=∠B,且∠BMF=180°﹣∠B﹣∠BFM,∠ACB=180°﹣∠B﹣∠BAC,
∴∠BMF=∠ACB,
∴∠BMF=∠ADN,
∴∠BMF+∠B=∠ADN+∠ADC,
∴∠MFC=∠NDC,且CF=CD,∠FCM=∠DCN,
∴△MFC≌△NDC(ASA)
∴CM=CN,
∴CM=2CG.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
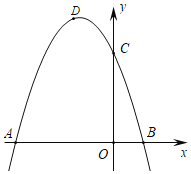
【题目】如图,抛物线C1的图象与x轴交A(﹣3,0),B(1,0)两点,与y轴交于点C(0,3)点D为抛物线的顶点.
(1)求抛物线C1的解析式;
(2)将抛物线C1关于直线x=1对称后的抛物线记为C2,将抛物线C1关于点B对称后的抛物线记为C3,点E为抛物线C3的顶点,在抛物线C2的对称轴上是否存在点F,使得△BEF为等腰三角形?若存在请求出点F的坐标,若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
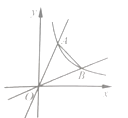
【题目】如图,在平面直角坐标系中,反比例函数![]() (x>0)与正比例函数y=kx、
(x>0)与正比例函数y=kx、 ![]() (k>1)的图象分别交于点A、B,若∠AOB=45°,则△AOB的面积是________.
(k>1)的图象分别交于点A、B,若∠AOB=45°,则△AOB的面积是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为方便住校生晚自习后回到宿舍就寝,新安装了一批照明路灯;一天上午小刚在观看新安的照明灯时,发现在太阳光的正面照射下,照明灯的灯杆的投影的末端恰好落在2.5米高文化走廊墙的顶端,小刚测得照明灯的灯杆的在太阳光下的投影从灯杆的杆脚到文化走廊的墙脚的影长为4.6米,同一时刻另外一个前来观看照明路灯小静测得身高1.5米小刚站立时在太阳光下的影长恰好为1米,请同学们画出与问题相关联的线条示意图并求出新安装的照明路灯的灯杆的高度?
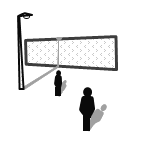
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B分别在函数y=![]() (k1>0)与函数y=
(k1>0)与函数y=![]() (k2<0)的图象上,线段AB的中点M在x轴上,△AOB的面积为4,则k1﹣k2的值为( )
(k2<0)的图象上,线段AB的中点M在x轴上,△AOB的面积为4,则k1﹣k2的值为( )

A.2B.4C.6D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=75°,∠C=45°,BC=4,点M是AC边上的动点,点M关于直线AB、BC的对称点分别为P、Q,则线段PQ长的取值范围是______.
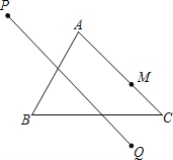
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小雪设计的“作以已知线段为斜边的等腰直角三角形”的尺规作图过程.
![]()
已知:线段AB.
求作:以AB为斜边的一个等腰直角△ABC.
作法:
(1)分别以点A和点B为圆心,大于![]() AB的长为半径作弧,两弧相交于P、Q两点;
AB的长为半径作弧,两弧相交于P、Q两点;
(2)作直线PQ,交AB于点O;
(3)以O为圆心,OA的长为半径作圆,交直线PQ于点C;
(4)连接AC,BC.
则△ABC即为所求作的三角形.根据小雪设计的尺规作图过程:
(1)使用直尺和圆规补全图形(保留作图痕迹);
(2)完成下面的证明:
证明:∵PA=PB,QA=QB,∴PQ垂直平分AB( )
在⊙O中,
∵AB为直径,∴∠ACB=90°( )
又∵∠AOC=∠BOC=90°,∴AC=BC( ),∴△ABC为以AB为斜边的等腰直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=-x2+mx的对称轴为直线x=2,若关于x的-元二次方程-x2+mx-t=0 (t为实数)在l<x<3的范围内有解,则t的取值范围是( )

A.-5<t≤4 B.3<t≤4 C.-5<t<3 D.t>-5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com