
分析 根据方程①与②有一个相同实数根进而使两方程相等,代入求出即可,再利用十字相乘法解①,得出方程的解,进而得出答案.
解答 解:当方程①与②有一个相同实数根,
则x2-(k+1)x+k=kx2-(k+2)x+k,
整理得:(1-k)x2+x=0,
则x[(1-k)x+1]=0,
故x1=0,x2=$\frac{1}{k-1}$,
当x=0时,则代入x2-(k+1)x+k=0得:k=0,
故k为0时,方程①与②有一个相同实数根,
x2-(k+1)x+k=0
(x-1)(x-k)=0,
解得:x1=1,x2=k,
则方程②的有一个解为1时,代入①②可得k=2,
综上所述:k为0或2时,方程①与②有一个相同实数根.
点评 本题考查了一元二次方程的解:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:选择题
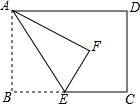 如图,在矩形ABCD中,点E为BC边上一点,连接AE,将△ABE沿AE折叠得到△AFE,且EF的延长线恰好经过点D,若BE=2,CE=3,则AE的长为( )
如图,在矩形ABCD中,点E为BC边上一点,连接AE,将△ABE沿AE折叠得到△AFE,且EF的延长线恰好经过点D,若BE=2,CE=3,则AE的长为( )| A. | 2$\sqrt{6}$ | B. | 5 | C. | 2$\sqrt{5}$ | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com