
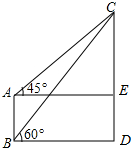
 如图:从B处测得建筑物上旗杆EC顶点C的仰角是60°,再从B的正上方40米高层上A处,测得C的仰角是45°,那么旗杆顶点C离地CD的高度是( )米.
如图:从B处测得建筑物上旗杆EC顶点C的仰角是60°,再从B的正上方40米高层上A处,测得C的仰角是45°,那么旗杆顶点C离地CD的高度是( )米.| A. | 18$\sqrt{3}$+40 | B. | 19$\sqrt{3}$+50 | C. | 20$\sqrt{3}$+60 | D. | 21$\sqrt{3}$+70 |
分析 设CE=x,在Rt△ACE中可得AE=x,在Rt△CBD中,解直角三角形可得x的值,继而可得CD的高度.
解答 解:设CE=x,
在Rt△ACE中,∵∠CAE=45°,
∴AE=CE=x,
∴BD=x,
在Rt△CBD中,tan∠CBD=$\frac{CD}{BD}$=$\frac{x+40}{x}$=$\sqrt{3}$,
解得:x=20$\sqrt{3}$+20,
则CD=CE+DE=20$\sqrt{3}$+60.
故选C.
点评 本题考查了解直角三角形的应用,关键要了解角之间的关系,找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作高或垂线构造直角三角形,另当问题以一个实际问题的形式给出时,要善于读懂题意,把实际问题划归为直角三角形中边角关系问题加以解决.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:初中数学 来源: 题型:解答题
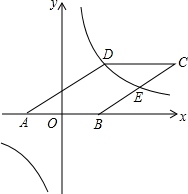 如图,在平面直角坐标系中有一个?ABCD,其中点A(-2,0),B(2,0),C(6,4),已知反比例函数y=$\frac{k}{x}$的图象恰好经过点D.点P是该反比例函数图象上的一个动点,且点P在该反比例函数图象上的第一象限内,当S△PAB=S△ODE时(两三角形面积相等),求点P的坐标.
如图,在平面直角坐标系中有一个?ABCD,其中点A(-2,0),B(2,0),C(6,4),已知反比例函数y=$\frac{k}{x}$的图象恰好经过点D.点P是该反比例函数图象上的一个动点,且点P在该反比例函数图象上的第一象限内,当S△PAB=S△ODE时(两三角形面积相等),求点P的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知四个数:a=(-2)2,b=-(-2),c=(-1)2013,d=-|-3|.
已知四个数:a=(-2)2,b=-(-2),c=(-1)2013,d=-|-3|.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AC,BD为⊙O的两条弦,AC,BD相交于点P,
如图,AC,BD为⊙O的两条弦,AC,BD相交于点P,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com