
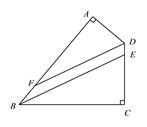
【题目】如图,四边形![]() 中,
中, ![]() ,
, ![]() 平分
平分![]() 交
交![]() 于
于![]() ,
, ![]() 平分
平分![]() 交
交![]() 于
于![]() .
.
求证: ![]()
【答案】证明见解析.
【解析】试题分析: 由四边形的内角和为360度求出∠ADC+∠ABC度数,由DF、BE分别为角平分线,利用角平分线定义及等量代换得到∠ABE+∠FDC为90度,再由直角三角形ADF两锐角互余及∠ADF=∠FDC,利用等量代换得到一对同位角相等,利用同位角相等两直线平行即可得证.
试题解析:
在四边形ABCD中
∠A+∠ABC+∠C+∠ADC=360°
又∵ ∠A=∠ C=90°
∴∠ABC+∠ ADC=180°
在Rt△AFD中,∠AFD+∠ADF=90°
又∵DF平分∠ADC
∴∠ADF=![]() ∠ADC
∠ADC
所以∠AFD=90°-![]() ∠ADC=
∠ADC=![]() ∠ABC
∠ABC
又∵BE平分∠ABC
∴∠ABE=![]() ∠ABC
∠ABC
∴∠AFD=∠ABE
∴BE//DF


科目:初中数学 来源: 题型:
【题目】某花卉种植基地欲购进甲、乙两种君子兰进行培育,若购进甲种2株,乙种3株,则共需成本1700元 ;若购进甲种3株,乙种1株,则共需成本1500元,
(1)求甲乙两种君子兰每株成本多少元?
(2)该种植基地决定在成本不超过30000元的前提下购进甲乙两种君子兰,若购进乙种君子兰的株数比甲种君子兰的3倍还多10株,求最多购进甲种君子兰多少株?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由a+3=b变为2(a+3)-5=2b-5,其过程中所用等式的性质及顺序是( )
A. 先用等式的性质1,再用等式的性质2
B. 先用等式的性质2,再用等式的性质1
C. 仅用了等式的性质1
D. 仅用了等式的性质2
查看答案和解析>>
科目:初中数学 来源: 题型:
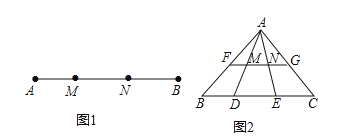
【题目】定义:如图1,点M,N把线段AB分割成AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点.
请解决下列问题:
(1)已知点M,N是线段AB的勾股分割点,且BN>MN>AM.若AM=2,MN=3,求BN的长;
(2)如图2,若点F、M、N、G分别是AB、AD、AE、AC边上的中点,点D,E是线段BC的勾股分割点,且EC>DE>BD,求证:点M,N是线段FG的勾股分割点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A是数轴上表示-30的点,B是数轴上表示10的点,C是数轴上表示18的点,点A,B,C在数轴上同时向数轴的正方向运动,点A运动的速度是6个单位长度每秒,点B和C运动的速度是3个单位长度每秒.设三个点运动的时间为t秒(t≠5),设线段OA的中点为P,线段OB的中点为M,线段OC的中点为N,当2PM-PN=2时,t的值为_____.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com