
【题目】如图,矩形OABC在平面直角坐标系xOy中,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=4,OC=3,若抛物线的顶点在BC边上,且抛物线经过O,A两点,直线AC交抛物线于点D.

(1)求抛物线的解析式;
(2)求点D的坐标;
(3)若点M在抛物线上,点N在x轴上,是否存在以A,D,M,N为顶点的四边形是平行四边形?若存在,求出点N的坐标;若不存在,请说明理由.
【答案】(1)y =-![]() x2+3x;(2) 点D坐标为(1,
x2+3x;(2) 点D坐标为(1,![]() );(3) 满足条件的点N有四个:N1(2,0),N2(6,0),N3(-
);(3) 满足条件的点N有四个:N1(2,0),N2(6,0),N3(-![]() -1,0),N4(
-1,0),N4(![]() -1,0).
-1,0).
【解析】
试题分析:(1)由OA的长度确定出A的坐标,再利用对称性得到顶点坐标,设出抛物线的顶点形式y=a(x-2)2+3,将A的坐标代入求出a的值,即可确定出抛物线解析式;
(2)设直线AC解析式为y=kx+b,将A与C坐标代入求出k与b的值,确定出直线AC解析式,与抛物线解析式联立即可求出D的坐标;
(3)存在,分两种情况考虑:如图所示,当四边形ADMN为平行四边形时,DM∥AN,DM=AN,由对称性得到M(3,![]() ),即DM=2,故AN=2,根据OA+AN求出ON的长,即可确定出N的坐标;当四边形ADM′N′为平行四边形,可得三角形ADQ全等于三角形N′M′P,M′P=DQ=
),即DM=2,故AN=2,根据OA+AN求出ON的长,即可确定出N的坐标;当四边形ADM′N′为平行四边形,可得三角形ADQ全等于三角形N′M′P,M′P=DQ=![]() ,N′P=AQ=3,将y=-
,N′P=AQ=3,将y=-![]() 代入得:-
代入得:-![]() =-
=-![]() x2+3x,求出x的值,确定出OP的长,由OP+PN′求出ON′的长即可确定出N′坐标.
x2+3x,求出x的值,确定出OP的长,由OP+PN′求出ON′的长即可确定出N′坐标.
试题解析:(1)设抛物线顶点为E,根据题意OA=4,OC=3,得:E(2,3),
设抛物线解析式为y=a(x-2)2+3,
将A(4,0)坐标代入得:0=4a+3,即a=-![]() ,
,
则抛物线解析式为y=-![]() (x-2)2+3=-
(x-2)2+3=-![]() x2+3x;
x2+3x;
(2)设直线AC解析式为y=kx+b(k≠0),
将A(4,0)与C(0,3)代入得:![]() ,
,
解得: ,
,
故直线AC解析式为y=-![]() x+3,
x+3,
与抛物线解析式联立得: ,
,
解得:![]() 或
或![]() ,
,
则点D坐标为(1,![]() );
);
(3)存在,分两种情况考虑:
①当点M在x轴上方时,如答图1所示:

四边形ADMN为平行四边形,DM∥AN,DM=AN,
由对称性得到M(3,![]() ),即DM=2,故AN=2,
),即DM=2,故AN=2,
∴N1(2,0),N2(6,0);
②当点M在x轴下方时,如答图2所示:

过点D作DQ⊥x轴于点Q,过点M作MP⊥x轴于点P,可得△ADQ≌△NMP,
∴MP=DQ=![]() ,NP=AQ=3,
,NP=AQ=3,
将yM=-![]() 代入抛物线解析式得:-
代入抛物线解析式得:-![]() =-
=-![]() x2+3x,
x2+3x,
解得:xM=2-![]() 或xM=2+
或xM=2+![]() ,
,
∴xN=xM-3=-![]() -1或
-1或![]() -1,
-1,
∴N3(-![]() -1,0),N4(
-1,0),N4(![]() -1,0).
-1,0).
综上所述,满足条件的点N有四个:N1(2,0),N2(6,0),N3(-![]() -1,0),N4(
-1,0),N4(![]() -1,0).
-1,0).


科目:初中数学 来源: 题型:
【题目】为了保护环境,某开发区综合治理指挥部决定购买A,B两种型号的污水处理设备共10台.已知用90万元购买A型号的污水处理设备的台数与用75万元购买B型号的污水处理设备的台数相同,每台设备价格及月处理污水量如下表所示:
污水处理设备 | A型 | B型 |
价格(万元/台) | m | m-3 |
月处理污水量(吨/台) | 220 | 180 |
(1)求m的值;
(2)由于受资金限制,指挥部用于购买污水处理设备的资金不超过165万元,问有多少种购买方案?并求出每月最多处理污水量的吨数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将6-(+3)-(-7)+(-2)写成省略加号的和的形式为( )
A.-6-3+7-2 B.6-3-7-2 C.6-3+7-2 D.6+3-7-2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=﹣![]() x+2与抛物线y=a(x+2)2相交于A、B两点,点A在y轴上,M为抛物线的顶点.
x+2与抛物线y=a(x+2)2相交于A、B两点,点A在y轴上,M为抛物线的顶点.
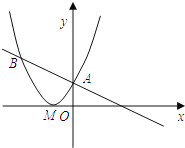
(1)请直接写出点A的坐标及该抛物线的解析式;
(2)若P为线段AB上一个动点(A、B两端点除外),连接PM,设线段PM的长为![]() ,点P的横坐标为x,请求出
,点P的横坐标为x,请求出![]() 与x之间的函数关系,并直接写出自变量x的取值范围;
与x之间的函数关系,并直接写出自变量x的取值范围;
(3)在(2)的条件下,线段AB上是否存在点P,使以A、M、P为顶点的三角形是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com