
【题目】已知![]() ,
, ![]() ,点
,点![]() 点
点![]() 分别在射线
分别在射线![]() ,射线
,射线![]() 上,若点
上,若点![]() 与点
与点![]() 关于
关于![]() 对称,点
对称,点![]() 点
点![]() 关于
关于![]() 对称,
对称, ![]() 与
与![]() 相交于点
相交于点![]() ,有以下命题:①
,有以下命题:①![]() ;②
;②![]() ;③若
;③若![]() ,
, ![]() ;④
;④![]() 是等腰直角三角形,则正确的命题有( ).
是等腰直角三角形,则正确的命题有( ).

A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC, ∠ABC、∠ACB的三等分线交于点E、D,若∠BFC=132°,∠BGC=118°,则∠A的度数为( )

A. 65° B. 66° C. 70° D. 78°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是由边长为1个单位长度的小正方形组成的网格图.
(1)请在图中建立平面直角坐标系,使A、B两点的坐标分别为A(2,3)、B(-2,0);
(2)正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫做格点三角形,在图中画出格点△ABC使得AB=AC,请写出在(1)中所建坐标系内所有满足条件的点C的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB=7°,一条光线从点A出发后射向OB边.若光线与OB边垂直,则光线沿原路返回到点A,此时∠A=90°-7°=83°.当∠A<83°时,光线射到OB边上的点A1后,经OB反射到线段AO上的点A2,易知∠1=∠2.若A1A2⊥AO,光线又会沿A2→A1→A原路返回到点A,此时∠A=76°.…若光线从A点出发后,经若干次反射能沿原路返回到点A,则锐角∠A的最小值为______.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
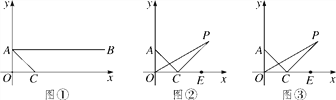
【题目】如图①,在平面直角坐标系中,A(0,1),B(4,1),C为x轴正半轴上一点,且AC平分∠OAB.
(1)求证:∠OAC=∠OCA;
(2)如图②,若分别作∠AOC的三等分线及∠OCA的外角的三等分线交于点P,即满足∠POC=![]() ∠AOC,∠PCE=
∠AOC,∠PCE=![]() ∠ACE,求∠P的大小;
∠ACE,求∠P的大小;
(3)如图③,在(2)中,若射线OP、CP满足∠POC=![]() ∠AOC,∠PCE=
∠AOC,∠PCE=![]() ∠ACE,猜想∠OPC的大小,并证明你的结论(用含n的式子表示).
∠ACE,猜想∠OPC的大小,并证明你的结论(用含n的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)已知△ABC是等边三角形,点D是直线BC上一点,以AD为一边在AD的右侧作等边△ADE.
(1)如图①,点D在线段BC上移动时,直接写出∠BAD和∠CAE的大小关系;
(2)如图②,点D在线段BC的延长线上移动时,猜想∠DCE的大小是否发生变化.若不变请求出其大小;若变化,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙三个登山爱好者经常相约去登山,今年1月甲参加了两次登山活动.
(1)1月1日甲与乙同时开始攀登一座900米高的山,甲的平均攀登速度是乙的1.2倍,结果甲比乙早15分钟到达顶峰.求甲的平均攀登速度是每分钟多少米?
(2)1月6日甲与丙去攀登另一座h米高的山,甲保持第(1)问中的速度不变,比丙晚出发0.5小时,结果两人同时到达顶峰,问甲的平均攀登速度是丙的多少倍?(用含h的代数式表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com