
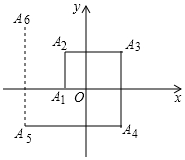
 如图,一个机器人从点O出发,向正西方向走2m到达点A1;再向正北方向走4m到达点A2;再向正东方向走6m到达点A3;再向正南方向走8m到达点A4;再向正西方向走10m到达点A5;…,按如此规律走下去,当机器人走到点A2017时,点A2017的坐标为(-2008,-2006),.
如图,一个机器人从点O出发,向正西方向走2m到达点A1;再向正北方向走4m到达点A2;再向正东方向走6m到达点A3;再向正南方向走8m到达点A4;再向正西方向走10m到达点A5;…,按如此规律走下去,当机器人走到点A2017时,点A2017的坐标为(-2008,-2006),.  新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
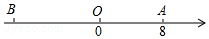
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
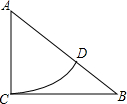 如图,在Rt△ABC中,∠ACB=90°,以点A为圆心,AC长为半径作圆弧交边AB于点D.若 AC=3,BC=4.则BD的长是( )
如图,在Rt△ABC中,∠ACB=90°,以点A为圆心,AC长为半径作圆弧交边AB于点D.若 AC=3,BC=4.则BD的长是( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
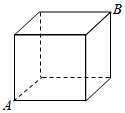 如图,一只昆虫在棱长为20cm的正方体的表面上爬行,则它从图中的顶点A爬到顶点B的最短距离为( )
如图,一只昆虫在棱长为20cm的正方体的表面上爬行,则它从图中的顶点A爬到顶点B的最短距离为( )| A. | 40cm | B. | 60cm | C. | $20\sqrt{5}cm$ | D. | $40\sqrt{3}cm$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
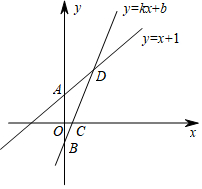 如图,已知直线y=x+1与y轴交于点A,一次函数y=kx+b的图象经过点B(0,-1),与x轴以及y=x+1的图象分别交于点C、D,且点D的坐标为(1,n).
如图,已知直线y=x+1与y轴交于点A,一次函数y=kx+b的图象经过点B(0,-1),与x轴以及y=x+1的图象分别交于点C、D,且点D的坐标为(1,n).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com