
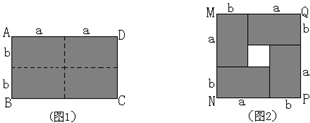
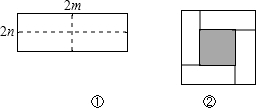
��ͼ1����һ����Ϊ2m����Ϊ2n�ij����Σ���ͼ�������ü���ƽ���ֳ��Ŀ�С�����Σ�Ȼ��ͼ2����״ƴ��һ�������Σ�
��1��ͼ2����Ӱ���ֵ����Ϊ����m��n��2����
��2���۲�ͼ2������д����������ʽ��m+n��2����m��n��2��mn֮��ĵ�����ϵʽ������m��n��2+4mn=��m+n��2����
��3�����ݣ�2���еĽ��ۣ���x+y=��6��xy=2.75����x��y=����5����
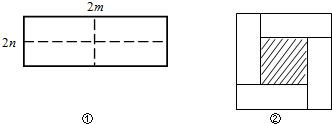
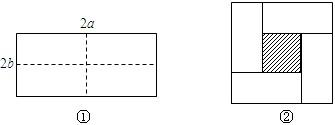
��4��������������ʽ������ͼ�ε��������ʾ����ͼ3������ʾ�ˣ�2m+n����m+n��=2m2+3mn+n2���Ի���һ������ͼ�Σ�ʹ��������ܱ�ʾ��m+n����m+3n��=m2+4mn+3n2��
��1����m��n��2 ��2����m��n��2+4mn=��m+n��2 ��3����5 ��4���𰸲�Ψһ
���������������1����ֱ���������ε������ʽ�õ���
��2������������ȫƽ����ʽ�������պ���������
��3������ɲ��յڶ��⣮
��4���ɲ���ͼ3���л�ͼ��
�⣺��1����m��n��2��3�֣�
��2����m��n��2+4mn=��m+n��2��3�֣�
��3����5��3�֣�
��4���𰸲�Ψһ����4�֣�
���磺
���㣺��ȫƽ����ʽ�ļ��α���
���������⿼������ȫƽ����ʽ�ı���֪ʶ������ؼ�������۲����и�����ͼʾ���ò�ͬ����ʽȥ��ʾ���������������ȫƽ����ʽ�����ܽ��б�ʽ��


 �ִʾ�ƪ��ͬ�����Ĵ��ϵ�д�
�ִʾ�ƪ��ͬ�����Ĵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
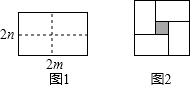 ��ͼ1����һ����Ϊ2m����Ϊ2n�ij����Σ���ͼ�������ü���������ֳ��ĸ���ȫ��ͬ��С�����Σ�Ȼ��ͼ2����״ƴͼ��
��ͼ1����һ����Ϊ2m����Ϊ2n�ij����Σ���ͼ�������ü���������ֳ��ĸ���ȫ��ͬ��С�����Σ�Ȼ��ͼ2����״ƴͼ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com