
【题目】某超市对![]() ,
,![]() 两种商品开展春节促销活动,活动方案有如下两种:
两种商品开展春节促销活动,活动方案有如下两种:
商品 |
|
| |
标价(单位:元) | 120 | 150 | |
方案一 | 每件商品出售价格 | 按标价打7折 | 按标价打 |
方案二 | 若所购商品超过10件(不同商品可累计)时,每件商品均按标价打8折后出售. | ||
(同一种商品不可同时参与两种活动)
(1)某单位购买![]() 商品5件,
商品5件,![]() 商品4件,共花费960元,求
商品4件,共花费960元,求![]() 的值;
的值;
(2)在(1)的条件下,若某单位购买![]() 商品
商品![]() 件(
件(![]() 为正整数),购买
为正整数),购买![]() 商品的件数比
商品的件数比![]() 商品件数的2倍还多一件,请问该单位该如何选择才能获得最大优惠?请说明理由.
商品件数的2倍还多一件,请问该单位该如何选择才能获得最大优惠?请说明理由.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,选择方案一才能获得最大优惠,当
时,选择方案一才能获得最大优惠,当![]() 时选择方案二才能获得最大优惠.
时选择方案二才能获得最大优惠.
【解析】
(1)先求出商品A和B每件的出售价格,再由其出售的件数和总费用即可列出关于![]() 的一元一次方程,求解即可;
的一元一次方程,求解即可;
(2)可知B商品购买的件数为![]() 件,表示出方案一和方案二的总费用,比较即可确定选择方案.
件,表示出方案一和方案二的总费用,比较即可确定选择方案.
解:(1)商品A每件的出售价格为![]() (元),商品B每件的出售价格为
(元),商品B每件的出售价格为![]() (元), 根据题意得:
(元), 根据题意得:![]()
解得![]()
所以![]() 的值为9.
的值为9.
(2)若某单位购买![]() 商品
商品![]() 件,则购买B商品
件,则购买B商品![]() 件,
件,
当![]() ,即
,即![]() 时,只能选择方案一得最大优惠
时,只能选择方案一得最大优惠
当![]() ,即
,即![]() 时,
时,
方案一中商品B每件的出售价格为![]() (元),总费用为
(元),总费用为![]() ;
;
方案二的总费用为![]() ,
,
![]()
![]() 当
当![]() 时选择方案二才能获得最大优惠,
时选择方案二才能获得最大优惠,
综合上述,当![]() 时,选择方案一才能获得最大优惠,当
时,选择方案一才能获得最大优惠,当![]() 时选择方案二才能获得最大优惠.
时选择方案二才能获得最大优惠.


科目:初中数学 来源: 题型:
【题目】数轴上有![]() 、
、![]() 、
、![]() 三个点对应的数分别是-22、-10、10.动点
三个点对应的数分别是-22、-10、10.动点![]() 从
从 ![]() 出发,以每秒3个单位的速度向点
出发,以每秒3个单位的速度向点![]() 方向移动,设移动时间为
方向移动,设移动时间为![]() 秒,点Q以每秒1个单位的速度向右运动,
秒,点Q以每秒1个单位的速度向右运动, ![]() 点到达
点到达![]() 点后,再立即按原速返回点
点后,再立即按原速返回点![]() .
.
![]()
(1)点![]() 到达点
到达点![]() 时
时![]() 秒,点
秒,点![]() 向右运动的过程所表示的数为 ,点
向右运动的过程所表示的数为 ,点![]() 返回的过程中所表示的数为 ;
返回的过程中所表示的数为 ;
(2)当![]() 为何值时,
为何值时, ![]() 、
、![]() 两点之间的距离为4.
两点之间的距离为4.
查看答案和解析>>
科目:初中数学 来源: 题型:
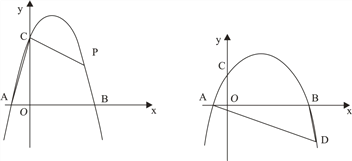
【题目】抛物线![]() 与x轴交于A,B两点(点A在点B的左边),与y轴正半轴交于点C.
与x轴交于A,B两点(点A在点B的左边),与y轴正半轴交于点C.
(1)如图1,若A(-1,0),B(3,0),
① 求抛物线![]() 的解析式;
的解析式;
② P为抛物线上一点,连接AC,PC,若∠PCO=3∠ACO,求点P的横坐标;
(2)如图2,D为x轴下方抛物线上一点,连DA,DB,若∠BDA+2∠BAD=90°,求点D的纵坐标.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
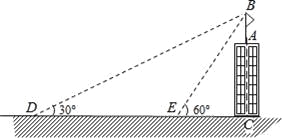
【题目】如图,某建筑物AC顶部有一旗杆AB,且点A,B,C在同一条直线上,小明在地面D处观测旗杆顶端B的仰角为30°,然后他正对建筑物的方向前进了20米到达地面的E处,又测得旗杆顶端B的仰角为60°,已知建筑物的高度AC=12m,求旗杆AB的高度(结果精确到0.1米).参考数据:![]() ≈1.73,
≈1.73,![]() ≈1.41.
≈1.41.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是边长为![]() 的正方形薄铁片,小明将其四角各剪去一个相同的小正方形(图中阴影部分)后,发现剩余的部分能折成一个无盖的长方体盒子,图2为盒子的示意图(铁片的厚度忽略不计).
的正方形薄铁片,小明将其四角各剪去一个相同的小正方形(图中阴影部分)后,发现剩余的部分能折成一个无盖的长方体盒子,图2为盒子的示意图(铁片的厚度忽略不计).
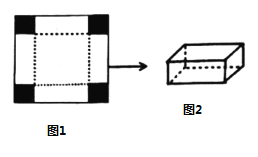
(1)设剪去的小正方形的边长为![]() ,折成的长方体盒子的容积为
,折成的长方体盒子的容积为![]() ,直接写出用只含字母
,直接写出用只含字母![]() 的式子表示这个盒子的高为______
的式子表示这个盒子的高为______![]() ,底面积为______
,底面积为______![]() ,盒子的容积
,盒子的容积![]() 为______
为______![]() ,
,
(2)为探究盒子的体积与剪去的小正方形的边长![]() 之间的关系,小明列表
之间的关系,小明列表
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 324 |
| 588 | 576 | 500 |
| 252 | 128 |
填空:①![]() ______,
______,![]() ______;
______;
②由表格中的数据观察可知当![]() 的值逐渐增大时,
的值逐渐增大时,![]() 的值______.(从“逐渐增大”,“逐渐减小”“先增大后减小”,“先减小后增大”中选一个进行填空)
的值______.(从“逐渐增大”,“逐渐减小”“先增大后减小”,“先减小后增大”中选一个进行填空)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点P是弦AC上一动点(不与A,C重合),过点P作PE⊥AB,垂足为E,射线EP交![]() 于点F,交过点C的切线于点D.
于点F,交过点C的切线于点D.

(1)求证:DC=DP;
(2)若∠CAB=30°,当F是![]() 的中点时,判断以A,O,C,F为顶点的四边形是什么特殊四边形?说明理由.
的中点时,判断以A,O,C,F为顶点的四边形是什么特殊四边形?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
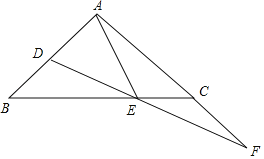
【题目】如图,△ABC中,AB=AC,∠BAC=90°,点D,E分别在AB,BC上,∠EAD=∠EDA,点F为DE的延长线与AC的延长线的交点.
(1)求证:DE=EF;
(2)判断BD和CF的数量关系,并说明理由;
(3)若AB=3,AE=![]() ,求BD的长.
,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
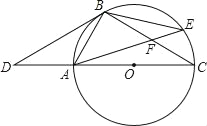
【题目】如图,点D是⊙O的直径CA延长线上一点,点B在⊙O上,且∠DBA=∠BCD.
(1)证明:BD是⊙O的切线.
(2)若点E是劣弧BC上一点,AE与BC相交于点F,且△BEF的面积为16,cos∠BFA=![]() ,那么,你能求出△ACF的面积吗?若能,请你求出其面积;若不能,请说明理由.
,那么,你能求出△ACF的面积吗?若能,请你求出其面积;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究证明:
(1)如图1,在△ABC中,AB=AC,点E是BC上的一个动点,EG⊥AB,EF⊥AC,CD⊥AB,点G,F,D分别是垂足.求证:CD=EG+EF;
猜想探究:
(2)如图2,在△ABC中,AB=AC,点E是BC的延长线上的一个动点,EG⊥AB于G,EF⊥AC交AC延长线于F,CD⊥AB于D,直接猜想CD、EG、EF之间的关系为 CD=EG﹣EF ;
问题解决:
(3)如图3,边长为10的正方形ABCD的对角线相交于点O、H在BD上,且BH=BC,连接CH,点E是CH上一点,EF⊥BD于点F,EG⊥BC于点G,则EF+EG= .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com