
分析 (1)根据平方差公式和零指数幂可以解答本题;
(2)先化简题目中的式子,再根据二次根式的加减法即可解答本题.
解答 解:(1)(2-$\sqrt{3}$)2013•(2+$\sqrt{3}$)2014-2|-$\frac{\sqrt{3}}{2}$|-(-$\sqrt{3}$)0
=$[(2-\sqrt{3})(2+\sqrt{3})]^{2013}•(2+\sqrt{3})$-2×$\frac{\sqrt{3}}{2}$-1
=$2+\sqrt{3}$-$\sqrt{3}$-1
=1;
(2)($\sqrt{48}$-4$\sqrt{\frac{1}{8}}$)-(3$\sqrt{\frac{1}{3}}$-2$\sqrt{0.5}$)
=$(4\sqrt{3}-\sqrt{2})-(\sqrt{3}-\sqrt{2})$
=$4\sqrt{3}-\sqrt{2}-\sqrt{3}+\sqrt{2}$
=$3\sqrt{3}$.
点评 本题考查二次根式的混合运算、零指数幂,解答本题的关键是明确它们各自的计算方法.


科目:初中数学 来源: 题型:填空题
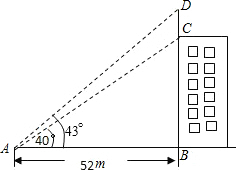 如图,∠BAD=43°,∠BAC=40°,AB=52m,求得避雷针CD的长约4.86m.(结果精确到0.1m)(可用下列参考数据求:sin43°≈0.68,sin40°≈0.64,cos43°≈0.73,cos40°≈0.76,tan43°≈0.93,tan40°≈0.84)
如图,∠BAD=43°,∠BAC=40°,AB=52m,求得避雷针CD的长约4.86m.(结果精确到0.1m)(可用下列参考数据求:sin43°≈0.68,sin40°≈0.64,cos43°≈0.73,cos40°≈0.76,tan43°≈0.93,tan40°≈0.84)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
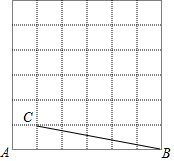 如图,是由边长相等的小正方形组成的网格,点A,B,C均在格点上,连接BC.
如图,是由边长相等的小正方形组成的网格,点A,B,C均在格点上,连接BC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
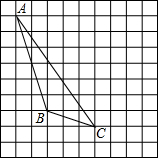 如图,在方格纸内将△ABC水平向右平移4个单位,再向下后平移1得到△A′B′C′.
如图,在方格纸内将△ABC水平向右平移4个单位,再向下后平移1得到△A′B′C′.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
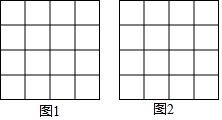 如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫做格点,请你以格点为顶点分别在图1和图2中画一个直角三角形,使它的三边长都是无理数.(两个三角形不全等)
如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫做格点,请你以格点为顶点分别在图1和图2中画一个直角三角形,使它的三边长都是无理数.(两个三角形不全等)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com