
【题目】已知![]() ,点
,点![]() 分别为两条平行线
分别为两条平行线![]() 上的一点,
上的一点,![]() 于
于![]() .
.
(1)如图1,直接写出![]() 和
和![]() 之间的数量关系;
之间的数量关系;
(2)如图2,连接![]() ,过点
,过点![]() 分别作
分别作![]() 和
和![]() 的角平分线交
的角平分线交![]() 于点
于点![]() ,
,![]() .
.
①求![]() 的度数;
的度数;
②探究![]() 和
和![]() 的数量关系并加以证明.
的数量关系并加以证明.

【答案】(1)![]() ,(2)①45°;②
,(2)①45°;②![]() ,证明见解析.
,证明见解析.
【解析】
(1)结论:∠ECD=90°+∠ABE.如图1中,过拐点作平行线,利用平行线性质即可得出结论;
(2) ①由![]() 和
和![]() 为
为![]() 和
和![]() 的角平分线,可得
的角平分线,可得![]() ,再由
,再由![]() ,通过角的运算即可得出结论.
,通过角的运算即可得出结论.
②由AB∥CD可得![]() ,再由
,再由![]() ,通过角的代换即可得出结论.
,通过角的代换即可得出结论.
解:(1)结论:![]() ,
,
理由:如图1中,从过G点作GH平行CD, 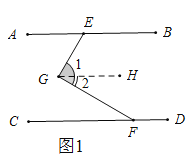
∵AB∥CD,
∴AB∥CD∥GH
∴∠AEG=∠1,∠CFG=∠2,
∵GE⊥GF,
∴∠CEH=90°,
∴∠ECD=∠H+∠CEH=90°+∠H,
∴∠ECD=90°+∠ABE.
(2)
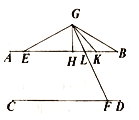
①∵![]()
∴![]() ,
,
∵![]() 和
和![]() 为
为![]() 和
和![]() 的角平分线,
的角平分线,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
②结论:![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠ACB与∠CAB的平分线交于点P,PD⊥AB于点D,若△APC与△APD的周长差为![]() ,四边形BCPD的周长为12+
,四边形BCPD的周长为12+![]() ,则BC等于______.
,则BC等于______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,平面直角坐标系xOy中,四边形OABC是矩形,点A,C的坐标分别为(6,0),(0,2).点D是线段BC上的一个动点(点D与点B,C不重合),过点D作直线y=-![]() x+b交折线O-A-B于点E.
x+b交折线O-A-B于点E.
(1)在点D运动的过程中,若△ODE的面积为S,求S与b的函数关系式,并写出自变量的取值范围;
(2)如图2,当点E在线段OA上时,矩形OABC关于直线DE对称的图形为矩形O′A′B′C′,C′B′分别交CB,OA于点D,M,O′A′分别交CB,OA于点N,E.求证:四边形DMEN是菱形;
(3)问题(2)中的四边形DMEN中,ME的长为____________.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】边长为1的正![]() 的顶点
的顶点![]() 在原点,点
在原点,点![]() 在
在![]() 轴负半轴上,正方形
轴负半轴上,正方形![]() 边长为2,点
边长为2,点![]() 在
在![]() 轴正半轴上,动点
轴正半轴上,动点![]() 从点
从点![]() 出发,以每秒1个单位的速度沿着
出发,以每秒1个单位的速度沿着![]() 的边按逆时针方向运动,动点
的边按逆时针方向运动,动点![]() 从
从![]() 点出发,以每秒1个单位的速度沿着正方形
点出发,以每秒1个单位的速度沿着正方形![]() 的边也按逆时针方向运动,点
的边也按逆时针方向运动,点![]() 比点
比点![]() 迟1秒出发,则点
迟1秒出发,则点![]() 运动2016秒后,则
运动2016秒后,则![]() 的值是___________.
的值是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(3,4),点B为直线x=1上的动点,设B(-1,y).

(1)如图①,若△ABO是等腰三角形且AO=AB时,求点B的坐标;
(2)如图②,若点C(x,0)且-1<x<3,BC⊥AC垂足为点C;
①当x=0时,求tan∠BAC的值;
②若AB与y轴正半轴的所夹锐角为α,当点C在什么位置时tanα的值最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某校七年级男生的体能情况,从该校七年级抽取50名男生进行1分钟跳绳测试,把所得数据整理后,画出频数分布直方图.已知图中从左到右第一、第二、第三、第四小组的频数的比为1:3:4:2.

(1)总体是 ,个体是 ,样本容量是 ;
(2)求第四小组的频数和频率;
(3)求所抽取的50名男生中,1分钟跳绳次数在100次以上(含100次)的人数占所抽取的男生人数的百分比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图1是AD∥BC的一张纸条,按图1→图2→图3,把这一纸条先沿EF折叠并压平,再沿BF折叠并压平,若图3中∠CFE=18°,则图2中∠AEF的度数为( )
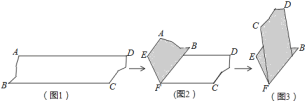
A.120°B.108°C.126°D.114°
查看答案和解析>>
科目:初中数学 来源: 题型:
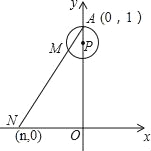
【题目】如图,在直角坐标系xOy中,已知点A(0,1),点P在线段OA上,以AP为半径的⊙P周长为1.点M从A开始沿⊙P按逆时针方向转动,射线AM交x轴于点N(n,0),设点M转过的路程为m(0<m<1).
(1)当m=![]() 时,n=_____;
时,n=_____;
(2)随着点M的转动,当m从![]() 变化到
变化到![]() 时,点N相应移动的路径长为_____.
时,点N相应移动的路径长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com