
科目:初中数学 来源: 题型:解答题
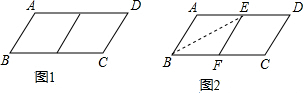 邻边不相等的平行四边形纸片,减去一个菱形,余下一个四边形,称为第一次操作,在余下的四边形纸片中再剪去一个菱形,余下一个四边形,称为第二次操作,…依此类推,若第n次余下的四边形是菱形,则称原平行四边形为n阶准菱形,如图1,平行四边形ABCD中,若AB=1,BC=2,则平行四边形ABCD为1阶准菱形.
邻边不相等的平行四边形纸片,减去一个菱形,余下一个四边形,称为第一次操作,在余下的四边形纸片中再剪去一个菱形,余下一个四边形,称为第二次操作,…依此类推,若第n次余下的四边形是菱形,则称原平行四边形为n阶准菱形,如图1,平行四边形ABCD中,若AB=1,BC=2,则平行四边形ABCD为1阶准菱形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在矩形ABCD中,AB=4,AD=6,点E是边BC的中点,连结AE,若将△ABE沿AE翻折,点B落在点F处,连结FC,则CF=( )
如图,在矩形ABCD中,AB=4,AD=6,点E是边BC的中点,连结AE,若将△ABE沿AE翻折,点B落在点F处,连结FC,则CF=( )| A. | $\frac{18}{5}$ | B. | $\frac{16}{5}$ | C. | $\frac{12}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
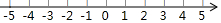 解不等式组$\left\{\begin{array}{l}{2(x+1)≥0,①}\\{1-\frac{x}{3}>\frac{x-3}{6},②}\end{array}\right.$并把解集在数轴上表示出来.
解不等式组$\left\{\begin{array}{l}{2(x+1)≥0,①}\\{1-\frac{x}{3}>\frac{x-3}{6},②}\end{array}\right.$并把解集在数轴上表示出来.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com