
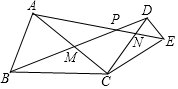
 如图,△ABC和△DCE均为等腰三角形,CA=CB,CD=CE,∠BCA=∠DCE.
如图,△ABC和△DCE均为等腰三角形,CA=CB,CD=CE,∠BCA=∠DCE.分析 (1)由CA=CB,CD=CE,∠ACB=∠DCE=α,利用SAS即可判定△ACD≌△BCE;
(2)根据△ACD≌△BCE,得出∠CBD=∠CAE,再根据∠APC=∠ACB,即可解决问题;
解答 (1)证明:解:(1)如图1,∵∠ACB=∠DCE=α,
∴∠BCD=∠ACE,
在△BCD和△ACE中,
$\left\{\begin{array}{l}{CB=CA}\\{∠BCD=∠ACE}\\{CD=CE}\end{array}\right.$,
∴△BCD≌△ACE(SAS),
∴BD=AE;
(2)解:∵CA=CB,
∴∠CAB=∠CBA=72°,
∴∠BCM=36°,
∵△BCD≌△ACE,
∴∠CBM=∠MAP,
∵∠BMC=∠AMP,
∴∠APM=∠BCM=36°,
∴∠BPE=144°.
点评 本题考查全等三角形的判定和性质、等腰三角形的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
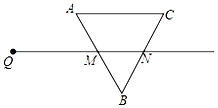 如图,射线QN与等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN,AM=MB=2 cm,QM=4 cm.动点P从Q出发,沿射线QN以每秒1 cm的速度向右移动,经过t秒,以点P为圆心,$\sqrt{3}$cm为半径的⊙P与△ABC的AB边相切(切点在边上),则t值为2或6秒.
如图,射线QN与等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN,AM=MB=2 cm,QM=4 cm.动点P从Q出发,沿射线QN以每秒1 cm的速度向右移动,经过t秒,以点P为圆心,$\sqrt{3}$cm为半径的⊙P与△ABC的AB边相切(切点在边上),则t值为2或6秒.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在正方形ABCD中,点E在边AD上,以DE为对角线构造正方形DGEF,点G在正方形ABCD内部,连接BF与边AD交于点M,连接CG.若DM=6,AM=4,则线段CG的长为$\frac{50}{7}$.
如图,在正方形ABCD中,点E在边AD上,以DE为对角线构造正方形DGEF,点G在正方形ABCD内部,连接BF与边AD交于点M,连接CG.若DM=6,AM=4,则线段CG的长为$\frac{50}{7}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -3 | B. | -2 | C. | 2 | D. | ±2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
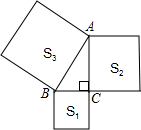 如图,以Rt△ABC的三边为边向外作正方形,其面积分别为S1,S2,S3,且S1=64,S3=289,则S2为( )
如图,以Rt△ABC的三边为边向外作正方形,其面积分别为S1,S2,S3,且S1=64,S3=289,则S2为( )| A. | 15 | B. | 225 | C. | 81 | D. | 25 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com