
【题目】如图一,∠ACB=90°,点D在AC上,DE⊥AB垂足为E,交BC的延长线于F,DE=EB,EG=EB, 
(1)求证:AG=DF;
(2)过点G作GH⊥AD,垂足为H,与DE的延长线交于点M,如图二  找出图中与AB相等的线段,并证明.
找出图中与AB相等的线段,并证明.
【答案】
(1)证明:∵DE=EB,EG=EB,DE⊥AB,
∴DE=EB=EB,
∴∠EGD=∠EGD=∠EDB=∠EBD=45°,
∴∠AGD=∠FDB=135°,
∵∠ACB=90°,∠AED=90°,∠ADE=∠FDC,
∴∠A=∠F,
∴∠ADG=∠FBD,
在△ADG和△FDB中 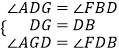
∴△ADG≌△FDB,
∴AG=DF
(2)解:∵DE=EB,EG=EB,
∴DE=EB=EB,∵DE⊥AB,
在△AED和△FEB中, 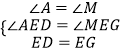
∴△AED≌△FEB,
∴AE=EM,
∴AE+EB=EM+DE,
即AB=DM
【解析】(1)根据已知条件得到DE=EB=EB,∠EGD=∠EGD=∠EDB=∠EBD=45°,进而证得∠AGD=∠FDB=135°,根据三角形内角和证得∠A=∠F,由三角形外角定理证得∠ADG=∠FBD,根据三角形的判定证得△ADG≌△FDB,由全等三角形的判定即可证得结论;(2)根据已知条件得到△AED≌△FEB,由全等三角形的性质得到AE=EM,即可得到结论.


 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】王阿姨销售草莓,草莓成本价为每千克10元,她发现当销售单价为每千克至少10元,但不高于每千克20元时,销售量y(千克)与销售单价x(元)的函数图象如图所示: 
(1)求y关于x的函数解析式,并写出它的定义域;
(2)当王阿姨销售草莓获得的利润为800元时,求草莓销售的单价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,AD是△ABC的内角平线,交BC于D点,DE⊥AB,DF⊥AC,垂足分别为E、F,连结EF,
(1)请根据上述几何语言,画出完整的图形,作∠BAC的角平分线AD要求尺规作图,(保留作图痕迹,不写作法);
(2)判断AD是否为EF的垂直平分线,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABC是等边三角形,D、E分别是BC、AC上一点,且AE=CD,AD,AD、BE交于P,过B作BQ⊥AD于Q,若QP=3cm,PE=1cm,求AD的长。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 ![]() ABC中,AD平分
ABC中,AD平分 ![]() BAC,按如下步骤作图:
BAC,按如下步骤作图:
第一步,分别以点A、D为圆心,以大于 ![]() AD的长为半径在AD两侧做弧,交于两点M、N;
AD的长为半径在AD两侧做弧,交于两点M、N;
第二步,连接MN分别交AB、AC于点E、F;
第三步,连接DE、DF.
若BD=6,AF=4,CD=3,则BE的长是( ).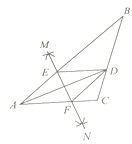
A.2
B.4
C.6
D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的5×5的方格纸中,每个小正方形的边长为1,点A、B、C均为格点(格点是指每个小正方形的顶点).
(1)按下列要求画图:
①标出格点D,使CD∥AB,并画出线段CD;
②标出格点E,使CE⊥AB,并画出线段CE.
(2)CD与CE的关系是 .
(3)计算△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,P是第一象限角平分线上的一点,且P点的横坐标为3.把一块三角板的直角顶点固定在点P处,将此三角板绕点P旋转,在旋转的过程中设一直角边与x轴交于点E,另一直角边与y轴交于点F,若△POE为等腰三角形,则点F的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与双曲线
与双曲线![]() 交于
交于![]() 两点,且点
两点,且点![]() 的横坐标为
的横坐标为![]() .
.

(1)求![]() 的值;
的值;
(2)若双曲线![]() 上一点
上一点![]() 的纵坐标为8,求
的纵坐标为8,求![]() 的面积;
的面积;
(3)过原点![]() 的另一条直线
的另一条直线![]() 交双曲线
交双曲线![]() 于
于![]() 两点(
两点(![]() 点在第一象限),若由点
点在第一象限),若由点![]() 为顶点组成的四边形面积为
为顶点组成的四边形面积为![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com