
【题目】《庄子·天下》:“一尺之棰,日取其半,万世不竭.”意思是说:一尺长的木棍,每天截掉一半,永远也截不完.我国智慧的古代人在两千多年前就有了数学极限思想,今天我们运用此数学思想研究下列问题.
(规律探索)
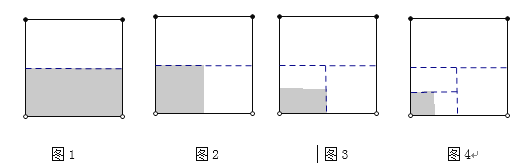
(1)如图1所示的是边长为1的正方形,将它剪掉一半,则S阴影1=1-![]() =__________;
=__________;
如图2,在图1的基础上,将阴影部分再裁剪掉—半,则S阴影2=1-![]() -(
-(![]() )2=_______;
)2=_______;
同种操作,如图3,S阴影3=1-![]() -(
-(![]() )2-(
)2-(![]() )3=__________;
)3=__________;
如图4,S阴影4=1-![]() -(
-(![]() )2-(
)2-(![]() )3-(
)3-(![]() )4=___________;
)4=___________;
……
若同种地操作n次,则S阴影n=1-![]() -(
-(![]() )2-(
)2-(![]() )3-…-(
)3-…-(![]() )n=_________.
)n=_________.
(规律归纳)
(2)直接写出![]() +
+![]() +
+![]() +…+
+…+![]() 的化简结果:_________.
的化简结果:_________.
(规律应用)
(3)直接写出算式![]() +
+![]() +
+![]() +…+
+…+![]() 的值:__________.
的值:__________.
【答案】(1)![]() ;
;![]() ;
;![]() ;
;![]() ;(
;(![]() )n;(2)
)n;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)结合图形计算即可求出,按照规律推出S阴影n的表达式即可;
(2)由上面的规律可得1-![]() -
-![]() -
-![]() -…-
-…-![]() =
=![]() ,然后转换得到
,然后转换得到![]() +
+![]() +
+![]() +…+
+…+![]() 再化简即可;
再化简即可;
(3)把(2)的化简结果计算即可得出.
(1)根据图像和计算直接可得S阴影1=1-![]() =
=![]() ;
;
S阴影2=1-![]() -(
-(![]() )2=
)2=![]() ;
;
S阴影3=1-![]() -(
-(![]() )2-(
)2-(![]() )3=
)3=![]() ;
;
S阴影4=1-![]() -(
-(![]() )2-(
)2-(![]() )3-(
)3-(![]() )4=
)4=![]() ;
;
由此可以发现规律1-![]() -(
-(![]() )2-(
)2-(![]() )3-…一直减下去,答案就等于减去的最后一个数的值;
)3-…一直减下去,答案就等于减去的最后一个数的值;
故S阴影n=1-![]() -(
-(![]() )2-(
)2-(![]() )3-…-(
)3-…-(![]() )n=(
)n=(![]() )n.
)n.
(2)由上面的规律可得1-![]() -
-![]() -
-![]() -…-
-…-![]() =
=![]() ,
,
即![]() +
+![]() +
+![]() +…+
+…+![]() =1-
=1-![]() =
=![]() .
.
(3) ![]() +
+![]() +
+![]() +…+
+…+![]() =1-
=1-![]() =
=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】国家规定“中小学生每天在校体育活动时间不低于1小时”.为此,某市就“每天在校体育活动时间”的问题随机抽样调查了321名初中学生.根据调查结果将学生每天在校体育活动时间t(小时)分成![]() ,
,![]() ,
,![]() ,
,![]() 四组,并绘制了统计图(部分).
四组,并绘制了统计图(部分).
![]() 组:
组:![]() 组:
组:![]() 组:
组:![]() 组:
组:![]()

请根据上述信息解答下列问题:
(1)![]() 组的人数是 ;
组的人数是 ;
(2)本次调查数据的中位数落在 组内;
(3)若该市约有12840名初中学生,请你估算其中达到国家规定体育活动时间的人数大约有多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
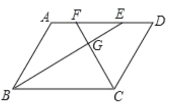
【题目】如图,在□ABCD中,∠ABC,∠BCD的平分线分别交AD于点E,F,BE,CF相交于点G.
(1)求证:BE⊥CF;
(2)若AB=a,CF=b,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,把R△ABC绕着B点逆时针旋转,得到Rt△DBE,点E在AB上 .
(1)若∠BDA=70°,求∠BAC的度数;
(2)若BC=8,AC=6,求△ABD中AD边上的高.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点A(0,2),B(4,0),C(4,3)三点.
(1)建立平面直角坐标系并描出A、B、C三点
(2)求△ABC的面积;
(3)如果在第二象限内有一点P(m,1),且四边形ABOP的面积是△ABC的面积的两倍;求满足条件的P点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数轴上5与﹣2所对的两点之间的距离:|5﹣(﹣2)|=7;
在数轴上﹣2与3所对的两点之间的距离:|﹣2﹣3|=5;
在数轴上﹣8与﹣5所对的两点之间的距离:|(﹣8)﹣(﹣5)|=3
在数轴上点A、B分别表示数a、b,则A、B两点之间的距离AB=|a﹣b|=|b﹣a|
回答下列问题:
(1)数轴上表示﹣2和﹣5的两点之间的距离是_____;
数轴上表示数x和3的两点之间的距离表示为_____;
数轴上表示数_____和_____的两点之间的距离表示为|x+2|,;
(2)七年级研究性学习小组在数学老师指导下,对式子|x+2|+|x﹣3|进行探究:
①请你在草稿纸上画出数轴,当表示数x的点在﹣2与3之间移动时,|x﹣3|+|x+2|的值总是一个固定的值为:_____.
②请你在草稿纸上画出数轴,要使|x﹣3|+|x+2|=7,数轴上表示点的数x=_____.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
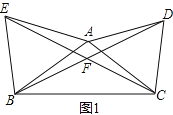
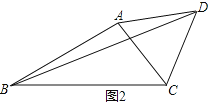
【题目】已知△ABC,以AC为边在△ABC外作等腰△ACD,其中AC=AD
(1) 如图1,若AB为边在△ABC外作△ABE,AB=AE,∠DAC=∠EAB=60°,求∠BFC的度数
(2) 如图2,∠ABC=α,∠ACD=β,BC=6,BD=8
① 若α=30°,β=60°,AB的长为
② 若改变α、β的大小,但α+β=90°,求△ABC的面积
查看答案和解析>>
科目:初中数学 来源: 题型:
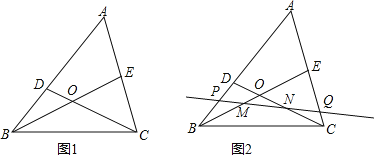
【题目】如图,在![]() 中,D、E分别为AB、AC上的点,线段BE、CD相交于点O,且
中,D、E分别为AB、AC上的点,线段BE、CD相交于点O,且![]() .
.
![]() 求证:
求证: ![]() ∽
∽![]() ;
;
![]() 求证:
求证: ![]() ;
;
![]() 若M、N分别是BE、CD的中点,过MN的直线交AB于P,交AC于Q,线段AP、AQ相等吗?为什么?
若M、N分别是BE、CD的中点,过MN的直线交AB于P,交AC于Q,线段AP、AQ相等吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某花店准备购进甲、乙两种花卉,若购进甲种花卉20盆,乙种花卉50盆,需要720元;若购进甲种花卉40盆,乙种花卉30盆,需要880元.
(1)求购进甲、乙两种花卉,每盆各需多少元?
(2)该花店销售甲种花卉每盆可获利6元,销售乙种花卉每盆可获利1元,现该花店准备拿出800元全部用来购进这两种花卉,设购进甲种花卉x盆,全部销售后获得的利润为W元,求W与x之间的函数关系式;
(3)在(2)的条件下,考虑到顾客需求,要求购进乙种花卉的数量不少于甲种花卉数量的6倍,且不超过甲种花卉数量的8倍,那么该花店共有几种购进方案?在所有的购进方案中,哪种方案获利最大?最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com