
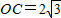 ,点T在线段OA上(不与线段端点重合),将纸片折叠,使点A落在射线AB上(记为点A′),折痕经过点T,折痕TP与射线AB交于点P,设点OT=t,折叠后纸片重叠部分(图中的阴影部分)的面积为S;
,点T在线段OA上(不与线段端点重合),将纸片折叠,使点A落在射线AB上(记为点A′),折痕经过点T,折痕TP与射线AB交于点P,设点OT=t,折叠后纸片重叠部分(图中的阴影部分)的面积为S;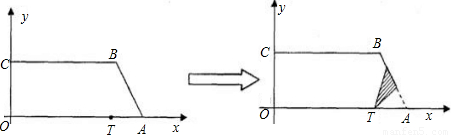
 ,
,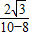 =
=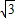 ,
,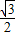 (10-t),A′P=AP=
(10-t),A′P=AP= AT=
AT= (10-t),
(10-t), A′P•TP=
A′P•TP=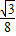 (10-t)2,
(10-t)2,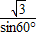 =4,
=4,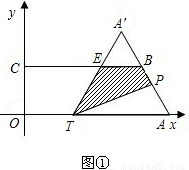
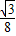 (10-t)2,
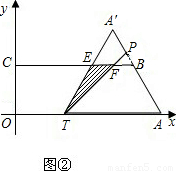
(10-t)2,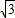 ;
;
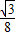 (10-t)2-
(10-t)2- (10-t-4)2×
(10-t-4)2×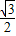 =
=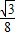 (-t2+4t+28)=-
(-t2+4t+28)=-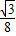 (t-2)2+4
(t-2)2+4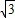 ,
,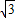 ;
; EF•OC=
EF•OC= ×4×2
×4×2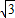 =4
=4 .
.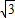 ,此时t的值是0<t≤2.
,此时t的值是0<t≤2.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 如图,把一张标准纸一次又一次对开,得到“2开”纸,“4开”纸,“8开”纸,“16开”纸….已知标准纸的短边长为a.
如图,把一张标准纸一次又一次对开,得到“2开”纸,“4开”纸,“8开”纸,“16开”纸….已知标准纸的短边长为a.
查看答案和解析>>
科目:初中数学 来源:2008年浙江省宁波市初中毕业升学统一考试、数学试卷 题型:044
如图1,把一张标准纸一次又一次对开,得到“2开”纸、“4开”纸、“8开”纸、“16开”纸….已知标准纸的短边长为a.

(1)如图2,把这张标准纸对开得到的“16开”张纸按如下步骤折叠:
第一步 将矩形的短边AB与长边AD对齐折叠,点B落在AD上的点B′处,铺平后得折痕AE;
第二步 将长边AD与折痕AE对齐折叠,点D正好与点E重合,铺平后得折痕AF.则AD:AB的值是________,AD、AB的长分别是________,________.
(2)“2开”纸、“4开”纸、“8开”纸的长与宽之比是否都相等?若相等,直接写出这个比值;若不相等,请分别计算它们的比值.
(3)如图3,由8个大小相等的小正方形构成“L”型图案,它的四个顶点E、F、G、H.
分别在“16开”纸的边AB、BC、CD、DA上,求DG的长.
(4)已知梯形MNPQ中,MN∥PQ,∠M=90°,MN=MQ=2PQ,且四个顶点M、N、P、Q都在“4开”纸的边上,请直接写出2个符合条件且大小不同的直角梯形的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,把一张标准纸一次又一次对开,得到“2开”纸,“4开”纸,“8开”纸,“16开”纸….已知标准纸的短边长为a.
如图,把一张标准纸一次又一次对开,得到“2开”纸,“4开”纸,“8开”纸,“16开”纸….已知标准纸的短边长为a.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com