
����Ŀ����֪����![]() +px+q��0����������
+px+q��0����������![]() ��
��![]() ����ô
����ô![]() +
+![]() ����p��
����p��![]()
![]() ��q�������������
��q�������������![]() +
+![]() ����p��
����p��![]()
![]() ��q����ô��
��q����ô��![]() ��
��![]() Ϊ������һԪ���η�����
Ϊ������һԪ���η�����![]() +px+q��0����������Ͻ��ۣ�����������⣺
+px+q��0����������Ͻ��ۣ�����������⣺
(1)��֪����x�ķ���![]() +mx+n��0(n��0)���������һԪ���η��̣�ʹ���������ֱ�����֪���������ĵ�����
+mx+n��0(n��0)���������һԪ���η��̣�ʹ���������ֱ�����֪���������ĵ�����
(2)��֪a��b����![]() ��15a��5��0��
��15a��5��0��![]() ��15b��5��0����
��15b��5��0����![]() ��ֵ��
��ֵ��
(3)��֪a��b��c��Ϊʵ������a+b+c��0��abc��16��������c����Сֵ
���𰸡���1��ny2+my+1=0����2��-47��2����3��c����СֵΪ4��
��������
��1�����跽��x2+mx+n=0����n��0�����������ֱ���x1��x2���ó�![]() +
+![]() =��
=��![]()
![]() =
=![]() ���ٸ������һԪ���η��̵��������ֱ�����֪���������ĵ����������������
���ٸ������һԪ���η��̵��������ֱ�����֪���������ĵ����������������
��2���������������������a��bʱ������a��b����a2��15a��5=0��b2��15b��5=0���ó�a��b��x2��15x��5=0�Ľ������a+b��ab��ֵ���������![]() ��ֵ������a=bʱ��ֱ�ӵó�����
��ֵ������a=bʱ��ֱ�ӵó�����
��3������a+b+c=0��abc=16���ó�a+b=��c��ab=![]() ��a��b�Ƿ���x2+cx+
��a��b�Ƿ���x2+cx+![]() =0�Ľ����ٸ���c2��4
=0�Ľ����ٸ���c2��4![]() ��0���������c����Сֵ��
��0���������c����Сֵ��
��1���跽��x2+mx+n=0����n��0�����������ֱ���x1��x2������![]() +
+![]() =
=![]() =��
=��![]()
![]() =
=![]() =
=![]() ����һ��һԪ���η��̵��������ֱ�����֪���������ĵ����������һԪ���η�������y2+
����һ��һԪ���η��̵��������ֱ�����֪���������ĵ����������һԪ���η�������y2+![]() y+
y+![]() =0����������ny2+my+1=0��
=0����������ny2+my+1=0��
��2���������������������a��bʱ����a��b����a2��15a��5=0��b2��15b��5=0����a��b��x2��15x��5=0�Ľ�����a+b=15��ab=��5����![]() =
=![]() =
=![]() =
=![]() =��47��
=��47��
�ڵ�a=bʱ��ԭʽ=2��
��3����a+b+c=0��abc=16����a+b=��c��ab=![]() ����a��b�Ƿ���x2+cx+
����a��b�Ƿ���x2+cx+![]() =0�Ľ�����c2��4
=0�Ľ�����c2��4![]() ��0��c2��
��0��c2��![]() ��0��
��0��
��c����������c3��43��0��c3��43��c��4��������c����Сֵ��4��


 ��У���˿��ֿ���ϵ�д�
��У���˿��ֿ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У�AB=6,BC=2,ֱ��l�dz�����ABCD��һ���Գ��ᣬ�ҷֱ���AD,BC���ڵ�E,F,��ֱ��l�ϵĶ���P,ʹ�á�PAB�͡�PBC��Ϊ����������.��P�ĸ�����_______��.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�ڡ�ABC�У�AB��AC��DΪBC��һ�㣬BE��CD��CF��BD����ô��EDF���ڣ�������
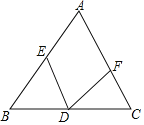
A.90������AB.90����![]() ��AC.45����
��AC.45����![]() ��AD.180������A
��AD.180������A
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ���ڡ�ABC�У���C����B��AD��AE�ֱ��ǡ�ABC�ĸߺͽ�ƽ���ߣ�
(1)����B��30�㣬��C��50�㣬���DAE�Ķ�����
(2)��DAE���C����B�кι�ϵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ������������������6�������Σ��١�ABC���ڡ�BCD���ۡ�BDE���ܡ�BFG���ݡ�FGH���ޡ�EFK.���Т�������������Ƶ���( )

A. �ڢۢ� B. �ۢܢ� C. �ܢݢ� D. �ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�O���ڽ��ı���ABCD�У�AB��AD����C��120�㣬��E�ڡ�O�ϣ�
(1)���AED�Ķ�����
(2)����O�İ뾶Ϊ2����![]() �ij�Ϊ���٣�
�ij�Ϊ���٣�
(3)����OD��OE������DOE��90��ʱ��AEǡ���ǡ�O���ڽ���n���ε�һ�ߣ���n��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�ǡ�O���ڽ������Σ�AB��AC����BCA��65������CD��AB��������O�ཻ�ڵ�D������BD�����DBC�Ĵ�СΪ

A. 15�� B. 35�� C. 25�� D. 45��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������ABCD�У���MAN=45��������BD��AM��AN�ֱ���E��F�㣬�����н�����ȷ����_____��
��MN=BM+DN
�ڡ�CMN���ܳ�����������ABCD�ı߳���������
��EF2=BE2+DF2��
����A��MN�ľ�����������εı߳�
�ݡ�AEN����AFM��Ϊ����ֱ�������Σ�
��S��AMN=2S��AEF
��S������ABCD��S��AMN=2AB��MN
����AB=a��MN=b����![]() ��2
��2![]() ��2��
��2��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ƽ��
ƽ��![]() ��
��![]() ��
��![]() ��.
��.

��1����ͼ�٣���![]() ��
��![]() �㣬
�㣬![]() ����
����![]() �Ķ�����
�Ķ�����
��2����ͼ�ڣ���![]() ��
��![]() ��
��![]() �㣬��֤��
�㣬��֤��![]() .
.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com