
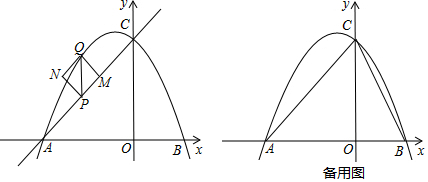
分析 (1)利用待定系数法求出抛物线的解析式;
(2)设Q点的坐标为(m,-$\frac{1}{2}$m2-m+4),表示出点P的坐标,根据正方形的面积公式和三角形的面积公式列出方程,解方程即可;
(3)根据相似三角形的性质定理得到比例式,解答即可.
解答 解:(1)对于y=x+4,
x=0时,y=4,点C的坐标为(0,4),
y=0时,x=-4,点A的坐标为(-4,0),
则$\left\{\begin{array}{l}{16a-4b+c=0}\\{4a+2b+c=0}\\{c=4}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=-1}\\{c=4}\end{array}\right.$,
则抛物线的解析式为y=-$\frac{1}{2}$x2-x+4;
(2)设Q点的坐标为(m,-$\frac{1}{2}$m2-m+4),
则点P的坐标为(m,m+4),
∴PQ=-$\frac{1}{2}$m2-m+4-(m+4)=-$\frac{1}{2}$m2-2m,
由题意得,$\frac{1}{2}$×(-$\frac{1}{2}$m2-2m)2=$\frac{1}{4}$×$\frac{1}{2}$×4×4,
整理得,-$\frac{1}{2}$m2-2m=±2,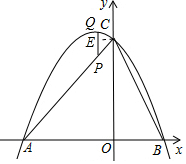
∵点Q在第二象限图象上,
∴-$\frac{1}{2}$m2-2m=2,-$\frac{1}{2}$m2-2m-2=0,
则(m+2)2=0,
解得,m1=m2=-2,
-$\frac{1}{2}$m2-m+4=4,
∴Q点的坐标为(-2,4);
(3)作CE⊥PQ于E,
设P点的坐标为(n,n+4),则Q点的坐标为(n,-$\frac{1}{2}$n2-n+4),
∵△PQC∽△ABC,
∴$\frac{CE}{OC}$=$\frac{PQ}{AB}$,即$\frac{-n}{4}$=$\frac{-\frac{1}{2}{n}^{2}-2n}{6}$,
解得,n=-1,
n+4=3,
则P点的坐标为(-1,3).
点评 本题考查的是二次函数的知识的综合应用、相似三角形的判定和性质、待定系数法的应用,掌握相似三角形的判定定理和性质定理、灵活运用数形结合思想是解题的关键.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:填空题
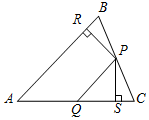 如图,在△ABC中,点P为BC中点,PR⊥AB,垂足为R,PS⊥AC,垂足为S,∠QPC=∠C,PR=PS,下面三个结论:①AS=AR②△BRP≌△CSP③QP∥AR中,正确的结论有①③.
如图,在△ABC中,点P为BC中点,PR⊥AB,垂足为R,PS⊥AC,垂足为S,∠QPC=∠C,PR=PS,下面三个结论:①AS=AR②△BRP≌△CSP③QP∥AR中,正确的结论有①③.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某水果经销商到水果种植基地采购葡萄,经销商一次性采购葡萄的采购单价y(元/千克)与采购量x(千克)之间的函数关系图象如图中折线AB→BC→CD所示(不包括端点A),
某水果经销商到水果种植基地采购葡萄,经销商一次性采购葡萄的采购单价y(元/千克)与采购量x(千克)之间的函数关系图象如图中折线AB→BC→CD所示(不包括端点A),查看答案和解析>>
科目:初中数学 来源: 题型:解答题
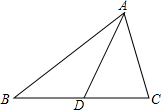 如图,△ABC中,AD是BC边上的中线,以D为旋转中心,将△ADC绕D旋转180°得到△EDB.
如图,△ABC中,AD是BC边上的中线,以D为旋转中心,将△ADC绕D旋转180°得到△EDB.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 将长方形纸片ABCD按图中方式折叠,其中EF、EC为折痕,折叠后A′、B′、E在一直线上,已知∠BEC=56度,那么∠A′EC=124度.
将长方形纸片ABCD按图中方式折叠,其中EF、EC为折痕,折叠后A′、B′、E在一直线上,已知∠BEC=56度,那么∠A′EC=124度.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
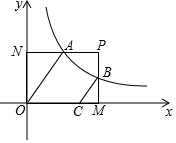 平面直角坐标系中,矩形OMPN的顶点P在第一象限,M在x轴上,N在y轴上,点A是PN的中点,且tan∠AON=$\frac{3}{4}$,过点A的双曲线y=$\frac{k}{x}$(x>0,k>0),与PM交于点B,过B作BC∥OA交x轴于C,若OC=$\frac{9}{2}$,则k=$\frac{972}{25}$.
平面直角坐标系中,矩形OMPN的顶点P在第一象限,M在x轴上,N在y轴上,点A是PN的中点,且tan∠AON=$\frac{3}{4}$,过点A的双曲线y=$\frac{k}{x}$(x>0,k>0),与PM交于点B,过B作BC∥OA交x轴于C,若OC=$\frac{9}{2}$,则k=$\frac{972}{25}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com