
����Ŀ��ij��ѧ�����ı��ѧ�����ƻ����һ���־�У�ᡢ������У�ᣮ�ƻ������ڲ����У���뽨����У
�Ṳ5000ƽ���ף���ʵʩ��Ϊ�����̻�������½�У��ֻ����˼ƻ���70���������У�����ƻ�
��20��������𡢽��������ǡ��Ϊ5000ƽ���ף�
��1����ԭ�ƻ��𡢽������������ƽ���ף�
��2���������У��ÿƽ����100Ԫ��������У��ÿƽ����500Ԫ����ʵ�ʲ𡢽��ķ��ù�����Ԫ��
���𰸡���1��ԭ�ƻ������У��3000ƽ���ף��½�У��2000ƽ���ף���2��ʵ�ʲ𡢽��ķ��ù�1060000Ԫ.
����������1��������ϵΪ�������У�����+������У�����=5000��ʵ�ʲ����У�����+ʵ�ʽ�����У�����=5000�� ��2��ʵ�ʲ𡢽��ķ���=ʵ�ʲ����У����Ǯ+ʵ�ʽ�����У����Ǯ��
���:��1����ԭ�ƻ������У��xƽ���ף��½�У��yƽ���ף�������ã�
![]()
���![]()
��2��ʵ�ʲ�����½�У����ù�Ϊ
3000����1+20������100��2000��70����500
��1060000
��ԭ�ƻ������У��3000ƽ���ף��½�У��2000ƽ���ף�ʵ�ʲ𡢽��ķ��ù�1060000Ԫ.


 ����ʦ��Сһ����ʦ������ҵϵ�д�
����ʦ��Сһ����ʦ������ҵϵ�д� ���100�ֵ�Ԫ�Ż�������ϵ�д�
���100�ֵ�Ԫ�Ż�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ֽƬABCD�У�EF��AD��M��N���߶�EF�����ȷֵ㣬���Ѹ�������ֽƬ����һ��Բ����ʹ��A���D�غϣ���ʱ������Բ��ֱ��Ϊ10cm����Բ����M��N�����ľ�����cm�� 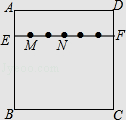
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�ı���ABCD�У���C=72�㣬��D=81�㣮��EF�۵��ı��Σ�ʹ��A��B�ֱ������ı����ڲ��ĵ�A�䡢B�䴦�����1+��2=�㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���˷���ʽ��̽����Ӧ�ã�
��1����ͼ1���������Ӱ���ֵ�������� ����д������ƽ�������ʽ����
��2���Ƚ�ͼ1��ͼ2��ͼ����Ӱ������������Եõ�
�˷���ʽ�� �� ����ʽ�ӱ����
��3�����������õ��Ĺ�ʽ���������и��⣺
����2m+n��p����2m��n+p�� ��10.3��9.7��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ݻ���վ�㳡�ƻ��ڹ㳡����ֲA��B���ֻ�ľ�� 6600�ã���A��ľ������B��ľ������2����600�ã�
��1��A��B���ֻ�ľ�������ֱ��Ƕ��ٿã�
��2������ִ�����26��ͬʱ��ֲ�����ֻ�ľ��ÿ��ÿ������ֲA��ľ60�û�B��ľ40�ã�Ӧ�ֱ��Ŷ�������ֲA��ľ��B��ľ������ȷ��ͬʱ��ɸ��Ե�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ʡ�������·��ˡ���ȫʡ��Сѧ���㷺���뿪չ��Լ��������֪ͨ��֪ͨ��Ҫ���ѧУȫ�������չ�������ж���.ij�н����ֶ��������Ϊ�˵���ѧ��������Լ���������ݵ��˽�̶�(�̶ȷ�Ϊ����A���˽�ܶ�������B���˽�϶�������C���˽����������D�����˽���)���Ա���һ����ѧ��ѧ�������˳������飬���ǽ���ε���Ľ�����Ƴ���������ͳ��ͼ.

����������Ϣ������������⣺
(1)���γ��������˶�����ѧ����
(2)��ȫ����ͳ��ͼ��
(3)������ѧ����1 800��ѧ�����������������ѧ������ѧ���У�������Լ�������������˽�϶������ж�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵȱ���ABC����һ��D��AD=5��BD=6��CD=4������ABD��A����ʱ����ת��ʹAB��AC�غϣ���D��ת����E������DCE�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
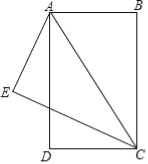
����Ŀ����ͼ����֪BA=AE=DC��AD=EC��CE��AE������ΪE��
��1����֤����DCA�ա�EAC��
��2��ֻ������һ���������� ����ʹ�ı���ABCDΪ���Σ������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ�κ���y��ax��b��y��bx��a��ͬһֱ������ϵ�е�ͼ�������( )


A. A B. B C. C D. D
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com