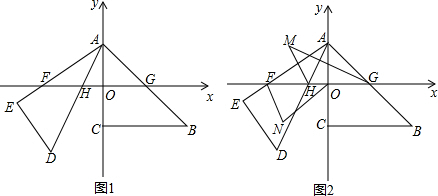
解:(1)∵AB∥ED
∴∠BAD=∠D=60°(两直线平行,内错角相等),
即∠BAC+∠CAD=60°.
∵∠BAC=45°,
∴∠CAD=60°-45°=15°,
∠AHO=90°-∠CAD=75°;
(2)①∵∠AHO+∠AHF=180°,∠AHO=60°,
∴∠AHF=180°-60°=120°
∵HM是∠AHF的平分线,
∴∠MHF=

∠AHF=60°(角平分线的定义).
∵GM是∠AGH的平分线,∠AGH=45°,
∴∠MGH=

∠AGH=22.5°,
∵∠MHF=∠MGH+∠M,
∴∠M=60°-22.5°=37.5°;
②∠N+∠M的度数不变,理由是:
当∠BAC与∠DAE没有重合部分时,
∠GAH-∠OAF=(45°+∠OAH)-(30°+∠OAH)=15°;
当AC与AD在一条直线上时,∠GAH-∠OAF=45°-30°=15°;
当∠BAC与∠DAE有重合部分时,
∠GAH-∠OAF=(45°-∠OAH)-(30°-∠OAH)=15°;
∴∠GAH-∠OAF=15°.
易得出∠M=∠MHF-∠MGH=

∠AHF-

∠AGH=

∠GAH,
∠N=180°-(

∠OFE+

90°)=180°-

(∠OAF+90°)-

90°
=90°-

∠OAF,
∴∠M+∠N=

∠GAH+90°-

∠OAF=90°+

×15°=97.5°(定值).
分析:(1)由AB∥ED可以得到∠BAD=∠D=60°,即∠BAC+∠CAD=60°,然后根据已知条件即可求出∠AHO;
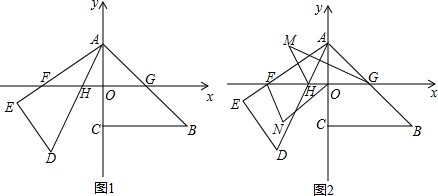
(2)①由∠AHO+∠AHF=180°,∠AHO=60°,可以求出∠AHF,而HM是∠AHF的平分线,GM是∠AGH的平分线,∠MHF=∠MGH+∠M,由此即可求出∠M;
②∠N+∠M的度数不变,当∠BAC与∠DAE没有重合部分时,∠GAH-∠OAF=(45°+∠OAH)-(30°+∠OAH)=15°;当AC与AD在一条直线上时,∠GAH-∠OAF=45°-30°=15°;当∠BAC与∠DAE有重合部分时,∠GAH-∠OAF=(45°-∠OAH)-(30°-∠OAH)=15°,即∠GAH-∠OAF=15°.而根据已知条件∠M=∠MHF-∠MGH=

∠AHF-

∠AGH=

∠GAH,∠N=180°-(

∠OFE+

90°)=180°-

(∠OAF+90°)-

90°=90°-

∠OAF,由此即可得到结论.
点评:此题比较复杂,考查了三角形的内角和、三角形的外角的性质、角平分线的性质、平行线的性质等多个知识,综合性比较强,难度比较大,学生首先心理上要相信自己,才能有信心解决问题.

 ∠AHF=60°(角平分线的定义).
∠AHF=60°(角平分线的定义). ∠AGH=22.5°,
∠AGH=22.5°, ∠AHF-
∠AHF- ∠AGH=
∠AGH= ∠GAH,
∠GAH, ∠OFE+
∠OFE+ 90°)=180°-
90°)=180°- (∠OAF+90°)-
(∠OAF+90°)- 90°
90° ∠OAF,
∠OAF, ∠GAH+90°-
∠GAH+90°- ∠OAF=90°+
∠OAF=90°+ ×15°=97.5°(定值).
×15°=97.5°(定值). ∠AHF-
∠AHF- ∠AGH=
∠AGH= ∠GAH,∠N=180°-(
∠GAH,∠N=180°-( ∠OFE+
∠OFE+ 90°)=180°-
90°)=180°- (∠OAF+90°)-
(∠OAF+90°)- 90°=90°-
90°=90°- ∠OAF,由此即可得到结论.
∠OAF,由此即可得到结论.

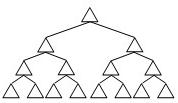 20、如图所示是一副“三角形图”,第一行有一个三角形,第二行有2个三角形,第三行有4个三角形,第四行有8个三角形,…,你是否发现三角形的排列规律,请写出第七行有
20、如图所示是一副“三角形图”,第一行有一个三角形,第二行有2个三角形,第三行有4个三角形,第四行有8个三角形,…,你是否发现三角形的排列规律,请写出第七行有