
 如图,点D,E分别在等边三角形ABC的边BC,AC上,BD=CE.则∠AFE的度数是( )
如图,点D,E分别在等边三角形ABC的边BC,AC上,BD=CE.则∠AFE的度数是( )| A. | 30° | B. | 60° | C. | 72° | D. | 80° |
分析 先证明△ABD≌△CBE,推出∠BAD=∠CBE,再由三角形的外角性质即可解决问题.
解答 解:∵△ABC是等边三角形,
∴∠ABD=∠BCE=60°,AB=AC,
在△ABD和△BCE中,$\left\{\begin{array}{l}{AB=BC}&{\;}\\{∠ABD=∠BCE}&{\;}\\{BD=CE}&{\;}\end{array}\right.$,
∴△ABD≌△BCE(SAS),
∴∠BAD=∠CBE,
∴∠AFE=∠BAD+∠ABF=∠CBE+∠ABF=∠ABD=60°,
故选:B.
点评 本题考查全等三角形的判定和性质、等边三角形的性质、三角形的外角性质;熟练掌握等边三角形的性质,证明三角形全等是解决问题的关键.


 巧学巧练系列答案
巧学巧练系列答案科目:初中数学 来源: 题型:选择题
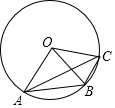 如图,A,B,C是⊙O上三个点,∠AOB=2∠BOC,则下列说法中正确的是( )
如图,A,B,C是⊙O上三个点,∠AOB=2∠BOC,则下列说法中正确的是( )| A. | ∠OBA=∠OCA | B. | 四边形OABC内接于⊙O | ||
| C. | AB=2BC | D. | ∠OBA+∠BOC=90° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 调查北海市市民的吸烟情况 | |
| B. | 调查北海市电视台某节目的收视率 | |
| C. | 调查北海市某校某班学生对“创建卫生城市”的知晓率 | |
| D. | 调查北海市市民家庭日常生活支出情况 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 39 | B. | 40 | C. | 41 | D. | 42 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
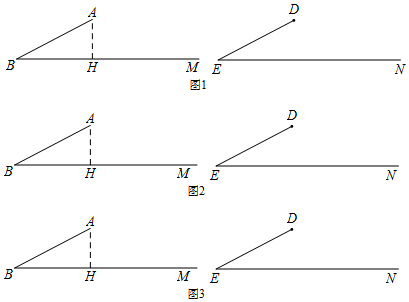
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com