
【题目】如图,AB是⊙O的直径,BT是⊙O的切线,若∠ATB=45°,AB=2,则阴影部分的面积是_____.
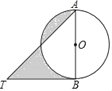
【答案】1
【解析】
设AT与圆O相交于点C,连接BC,根据切线的性质得到AB⊥TB,因为∠ATB=45°,得到∠TAB=45°=∠ATB,根据等腰直角三角形的性质得到AB=TB=2,根据直径所对的圆周角是直角得到∠ACB=90°,推出∠CAB=∠CBA=45°=∠ATB,AC=BC=TC,点C是弧ACB的中点,则S阴影=S△TCB,即可求解.
解:如图:设AT与圆O相交于点C,连接BC

∵BT是⊙O的切线
∴AB⊥TB,
又∵∠ATB=45°
∴∠TAB=45°=∠ATB
∴AB=TB=2
∵AB是直径
∴∠ACB=90°
∴∠CAB=∠CBA=45°=∠ATB
∴AC=BC=TC
∴点C是![]() 的中点
的中点
∴S阴影=S△TCB
∴S阴影=![]() S△ABT
S△ABT![]()
故答案为:1


科目:初中数学 来源: 题型:
【题目】在△ABC中,D为BC上一点,连接AD,过点B作BE垂直于CA的延长线于点E,BE与DA的延长线相交于点F.
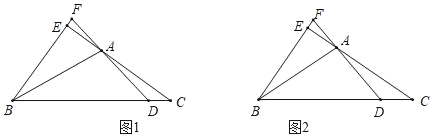
(1)如图1,若AB平分∠CBE,∠ADB=30°,AE=3,AC=7,求CD的长;
(2)如图2,若AB=AC,∠ADB=45°,求证;BC=![]() DF.
DF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某一天,水果经营户老张用1600元从水果批发市场批发猕猴桃和芒果共50千克,后再到水果市场去卖,已知猕猴桃和芒果当天的批发价和零售价如表所示:
品名 | 猕猴桃 | 芒果 |
批发价 | 20 | 40 |
零售价 | 26 | 50 |
![]() 他购进的猕猴桃和芒果各多少千克?
他购进的猕猴桃和芒果各多少千克?
![]() 如果猕猴桃和芒果全部卖完,他能赚多少钱?
如果猕猴桃和芒果全部卖完,他能赚多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 经过正方形网格中的格点
经过正方形网格中的格点![]() 、
、![]() 、
、![]() 、
、![]() ,请你仅用网格中的格点及无刻度的直尺分别在图1、图2、图3中画出一个满足下列两个条件的
,请你仅用网格中的格点及无刻度的直尺分别在图1、图2、图3中画出一个满足下列两个条件的![]() :
:
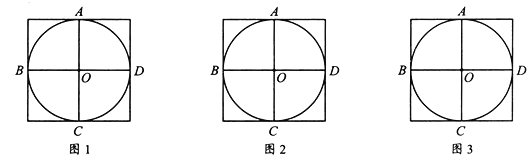
(1)顶点![]() 在
在![]() 上且不与点
上且不与点![]() 、
、![]() 、
、![]() 、
、![]() 重合;
重合;
(2)![]() 在图1、图2、图3中的正切值分别为1、
在图1、图2、图3中的正切值分别为1、![]() 、2.
、2.
查看答案和解析>>
科目:初中数学 来源: 题型:
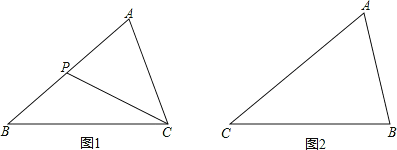
【题目】王华在学习相似三角形时,在北京市义务教育课程改革实验教材第17册书,第31页遇到这样一道题:
如图1,在△ABC中,P是边AB上的一点,联结CP.
要使△ACP∽△ABC,还需要补充的一个条件是____________,或_________.
请回答:
(1)王华补充的条件是____________________,或_________________.
(2)请你参考上面的图形和结论,探究、解答下面的问题:
如图2,在△ABC中,∠A=30°,AC2= AB2+AB.BC.
求∠C的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校两次购买足球和篮球的支出情况如表:
足球(个) | 篮球(个) | 总支出(元) | |
第一次 | 2 | 3 | 310 |
第二次 | 5 | 2 | 500 |
(1)求购买一个足球、一个篮球的花费各需多少元?(请列方程组求解)
(2)学校准备给帮扶的贫困学校送足球、篮球共计60个,恰逢市场对两种球的价格进行了调整,足球售价提高了10%,篮球售价降低了10%,如果要求一次性购得这批球的总费用不超过4000元,那么最多可以购买多少个足球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD和正方形DEFG中,点G在CD上,DE=2,将正方形DEFG绕点D顺时针旋转60°,得到正方形DE'F'G',此时点G'在AC上,连接CE',则CE'+CG'=______
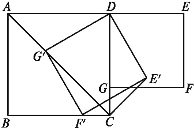
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A的坐标为(3,0),点C的坐标为(0,4),OABC为矩形,反比例函数![]() 的图象过AB的中点D,且和BC相交于点E,F为第一象限的点,AF=12,CF=13.
的图象过AB的中点D,且和BC相交于点E,F为第一象限的点,AF=12,CF=13.
(1)求反比例函数![]() 和直线OE的函数解析式;
和直线OE的函数解析式;
(2)求四边形OAFC的面积?
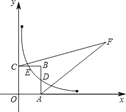
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在平面直角坐标系中,四边形OABC是菱形,点C的坐标为(3,4),平行于对角线AC的直线m从原点O出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线m与菱形OABC的两边分别交于点M、N,直线m运动的时间为t(秒).

(1)求点B的坐标;
(2)当MN=![]() AC时,求t的值;
AC时,求t的值;
(3)设△OMN的面积为S,求S与t的函数表达式,并确定S的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com