
【题目】某体育用品商店老板到体育商场批发篮球、足球、排球共![]() 个,得知该体育商场篮球、足球、排球平均每个
个,得知该体育商场篮球、足球、排球平均每个![]() 元,篮球比排球每个多
元,篮球比排球每个多![]() 元,排球比足球每个少
元,排球比足球每个少![]() 元.
元.
(1) 求出这三种球每个各多少元;
(2) 经决定,该老板批发了这三种球的任意两种共![]() 个,共花费了1060元,问该老板可能买了哪两种球?各买了几个;
个,共花费了1060元,问该老板可能买了哪两种球?各买了几个;
(3) 该老板打算将每一种球各提价![]() 元后,再进行打折销售,若排球、足球打八折,篮球打八五折,在(2)的情况下,为获得最大利润,他批发的一定是哪两种球?各买了几个?计算并说明理由.
元后,再进行打折销售,若排球、足球打八折,篮球打八五折,在(2)的情况下,为获得最大利润,他批发的一定是哪两种球?各买了几个?计算并说明理由.
【答案】(1)篮球每只40元,足球38元,排球30元;(2)若买的是足球和排球则求得可以是买足球20,排球10只;若买的是篮球和排球则是篮球16只,排球14只;(3)买篮球16只,排球14只利润最大.
【解析】
(1)分别设篮球每只x元,足球y,排球z,根据题意可得出三个二元一次不定方程,联立求解即可得出答案.
(2)假设:①买的是篮球和足球,分别为a只和b只,根据题意可得出两个方程,求出解后可判断出是否符合题意,进而再用同样的方法判断其他的符合题意的情况;
(3)分别对两种情况下的利润进行计算,然后比较利润的大小即可得出答案.
(1)设篮球每只x元,足球y,排球z,得
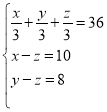 ;
;
解得x=40;y=38;z=30;
故篮球每只40元,足球38元,排球30元;
(2)假设:①买的是篮球和足球,分别为a只和b只,则
![]() ;
;
解得![]() ,则不可能是这种情况;
,则不可能是这种情况;
同理若买的是足球和排球则求得可以是买足球20,排球10只;
若买的是篮球和排球则是篮球16只,排球14只;
(3)对两种情况分别计算,若为足球和排球,即(38+20)×0.8×20+(30+20)0.8×10=1328(元);
若为篮球和排球,即(40+20)×0.85×16+(30+20)×0.8×14=1376(元),
∴买篮球16只,排球14只利润最大.


科目:初中数学 来源: 题型:
【题目】“安全教育,警钟长鸣”,某校随机抽取了部分学生就安全知识的了解情况进行问卷调查,其中“很好”“较好”“一般”“较差”四类学生分别占调查学生数的25%,50%,20%,5%.
(1)选择合适的统计图描述上面的数据;
(2)根据上面的调查结果,若该校有1400名学生,则对安全知识了解“较差”的学生有多少名?
(3)根据以上信息,请提出一条合理化建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且经A(1,0)、
B(0,﹣3)两点.(1)求抛物线的解析式;
(2)在抛物线的对称轴x=﹣1上,是否存在点M,使它到点A的距离与到点B的距离之和最小,如果存在求出点M的坐标,如果不存在请说明理由.
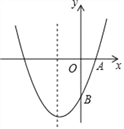
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,小亮一家在东昌湖游玩,妈妈在湖心岛岸边P处观看小亮与爸爸在湖中划船(如图).小船从P处出发,沿北偏东60°划行200米到达A处,接着向正南方向划行一段时间到达B处.在B处小亮观测妈妈所在的P处在北偏西37°方向上,这时小亮与妈妈相距多少米(精确到米)?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某面包店推出一款新口味面包,每个成本1.5元,售价5元/个,试营业期间一律8折,每天只生产50个,为保持面包新鲜,当天未卖完的当天销毁,试营业期间市场日需求量(即每天所需数量)如表所示:
天数 | 8 | 10 | 10 | 2 |
日需求量/个 | 45 | 48 | 51 | 56 |
(1)补充日销售量(即每天销售的数量)的条形统计图;
(2)试营业期间某天的日需求量为45个,求当天的利润;
(3)求试营业期间(30)天的总利润

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣![]() +bx+c与y轴交于点C,与x轴的两个交点分别为A(﹣4,0),B(1,0).
+bx+c与y轴交于点C,与x轴的两个交点分别为A(﹣4,0),B(1,0).
(1)求抛物线的解析式;
(2)已知点P在抛物线上,连接PC,PB,若△PBC是以BC为直角边的直角三角形,求点P的坐标;
(3)已知点E在x轴上,点F在抛物线上,是否存在以A,C,E,F为顶点的四边形是平行四边形?若存在,请直接写出点E的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点![]() 为直线
为直线![]() 上一点,过点
上一点,过点![]() 作射线
作射线![]() ,使
,使![]() ,将一把直角三角尺的直角顶点放在点
,将一把直角三角尺的直角顶点放在点![]() 处,一边
处,一边![]() 在射线
在射线![]() 上,另一边
上,另一边![]() 在直线
在直线![]() 的下方,其中
的下方,其中![]() .
.

(1)将图1中的三角尺绕点![]() 顺时针旋转至图2,使一边
顺时针旋转至图2,使一边![]() 在
在![]() 的内部,且恰好平分
的内部,且恰好平分![]() ,求
,求![]() 的度数;
的度数;
(2)将图1中三角尺绕点![]() 按每秒10的速度沿顺时针方向旋转一周,旋转过程中,在第 秒时,边
按每秒10的速度沿顺时针方向旋转一周,旋转过程中,在第 秒时,边![]() 恰好与射线
恰好与射线![]() 平行;在第 秒时,直线
平行;在第 秒时,直线![]() 恰好平分锐角
恰好平分锐角![]() .
.
(3)将图1中的三角尺绕点![]() 顺时针旋转至图3,使
顺时针旋转至图3,使![]() 在
在![]() 的内部,请探究
的内部,请探究![]() 与
与![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,∠BAD=60°.
(1)如图1,点E为线段AB的中点,连接DE,CE,若AB=4,求线段EC的长;
(2)如图2,M为线段AC上一点(M不与A,C重合),以AM为边,构造如图所示等边三角形AMN,线段MN与AD交于点G,连接NC,DM,Q为线段NC的中点,连接DQ,MQ,求证:DM=2DQ.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com