
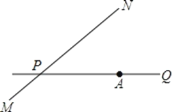
【题目】如图,公路 MN 和公路 PQ 在点 P 处交会,且∠QPN=30°.点 A 处有一所中学,AP=160m,一辆拖拉机从 P 沿公路 MN 前行,假设拖拉机行驶时周围 100m 以内会受到噪声影响,那么该所中学是否会受到噪声影响,请说明理由,若受影响,已知拖拉机的速度为 18km/h,那么学校受影响的时间为多长?
【答案】该所中学会受到噪声影响;学校受影响的时间为24秒
【解析】
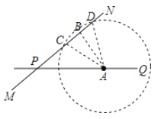
首先过点A作AB⊥MN于B,由∠QPN=30°,AP=160m,根据直角三角形中30°对的直角边是斜边的一半,即可求得AB的长,即可知该所中学是否会受到噪声影响;然后以A为圆心,100m为半径作圆,交MN于点C与D,由勾股定理,即可求得BC的长,继而可求得CD的长,则可求得学校受影响的时间.
过点A作AB⊥MN于B,
∵∠QPN=30°,AP=160m,
∴![]() ,
,
∵80<100,
∴该所中学会受到噪声影响;
以A为圆心,100m为半径作圆,交MN于点C与D,
则AC=AD=100m,
在Rt△ABC中,![]() ,
,
∵AC=AD,AB⊥MN,
∴BD=BC=60m,
∴CD=BC+BD=120m,
∵![]() ,
,
∴学校受影响的时间为:120÷5=24(秒).


科目:初中数学 来源: 题型:
【题目】已知二次函数![]() .
.
(![]() )将
)将![]() 化成
化成![]() 的形式.
的形式.
(![]() )与
)与![]() 轴的交点坐标是__________,与
轴的交点坐标是__________,与![]() 轴的交点坐标是__________.
轴的交点坐标是__________.
(![]() )在坐标系中利用描点法画出此抛物线.
)在坐标系中利用描点法画出此抛物线.
|
|
| |||||
|
|
|