Question

如图，四边形ABCD中，点E在边CD上，连结AE、BE．给出下列五个关系式：①AD∥BC；②DE＝CE；③∠1＝∠2；④∠3＝∠4；⑤AD＋BC＝AB．将其中的三个关系式作为题设，另外两个作为结论，构成一个命题．

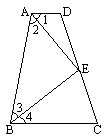
(1)用序号写出一个真命题(书写形式如：如果×××，那么××)，并给出证明；

(2)用序号再写出三个真命题(不要求证明)；

(3)真命题不止以上四个，想一想，就能够多写出几个真命题．

Answer 1

答案：
解析：

解(1)1)如果①②③，那么④⑤证明：如图，延长AE交BC的延长线于F 　　∵AD∥BC　　∴∠1＝∠F 　　又∵∠AED＝∠CEF，DE＝EC 　　∴△ADE≌△FCE 　　∴AD＝CF，AE＝EF 　　∵∠1＝∠F，∠1＝∠2，∴∠2＝∠F 　　∴AB＝BF　　∴∠3＝∠4 　　∴AD＋BC＝CF＋BC＝BF＝AB2)如果①②④，那么③⑤ 　　证明　　延长BE交AD的延长线于F，其证明方法与上类似，略． 　　3)如果①②⑤，那么③④ 　　证明　　仍如图，延长AE交BC的延长线于F． 　　由AD∥BC，DE＝CE．可证△ADE≌△FCE． 　　∴AD＝CF　　AE＝EF∵AD＋BC＝AB． 　　∴AB＝FB． 　　∴∠2＝∠F＝∠1，∠3＝∠4． 　　4)如果①③④，那么②⑤ 　　证明　　方法一：仍如图，延长AE交BC的延长线于F． 　　∵AD∥BC 　　∴∠1＝∠F∵∠1＝2 　　∴∠2＝∠F又∠3＝∠4　　BE＝BE　　∴△ABE≌△FBE 　　∴AE＝FE，AB＝FB 　　∴△ADE≌△FCE 　　∴AD＝FC　　DE＝CE．从而AD＋BC＝AB 　　此外，本命题也可以这样证明． 　　方法二：如图，在AB边上截取AK＝AD，连结KE∵AK＝AD，∠1＝∠2，AE＝AE， 　　∴△AKE≌△ADE 　　∴∠5＝∠6，KE＝DE∵AD∥BC，∠1＝∠2，∠3＝∠4 　　∴∠AEB＝ 　　∵∠6＋∠7＝∠5＋∠8． 　　∴∠7＝∠8． 　　∴△BKE≌△BCE． 　　∴BK＝BC，KE＝CE　　从而DE＝CE，AD＋BC＝AB． 　　5)如果①③⑤，那么②④ 　　证明　　如图(前两个)，均可证明．略． 　　6)如果①④⑤，那么②③ 　　证明　　方法同5)．略 　　7)如果②③⑤，那么①④ 　　证明　　如图，先证△AKE≌△ADE，再证△BKE≌△BCE，即可． 　　8)如果②④⑤，那么①③ 　　证明　　方法同7)． 　　9)如果③④⑤，那么①② 　　证明　　如图，也是先证△AKE≌△ADE，再证△BKE≌△BCE，即可． 　　2)在(1)中只要证明9个真命题中的1个，剩余的选3个纳入(2)． 　　(3)还有5个真命题供选择． 　　评析：对1)，如果①②③，那么④⑤，当然也可作图来证，不过有关这方面的知识(需证四点BCEK共圆)我们还没有学过．另外亦可作梯形的中位线ME，那要等到学过梯形的中位线定理后才能证明． 　　注意，10个命题中，如果②③④，那么①⑤是假命题．

提示：

思路与技巧：由五个关系式中三个关系式作为题设，另外两个作为结论，一共能构成10个命题，其中有些是真命题，有些是假命题．究竟哪些是真命题：一是靠推理，二是靠经验．