
分析 (1)先变形化为(x-2)2=$\frac{1}{4}$,然后直接开平方即可;
(2)方程两边加上9,利用完全平方公式变形,开方即可求出解.
(3)观察可得最简公分母是2(x-3),方程两边乘最简公分母,可以把分式方程转化为整式方程求解.
解答 解:(1)4(x-2)2=1
(x-2)2=$\frac{1}{4}$,
∴x-2=±$\frac{1}{2}$,
∴x1=$\frac{3}{2}$,x2=$\frac{5}{2}$.
(2)x2+6x=1
方程配方得:x2+6x+9=10,
即(x+3)2=10,
开方得:x+3=±$\sqrt{10}$,
解得:x1=-3+$\sqrt{10}$,x2=-3-$\sqrt{10}$.
(3)$\frac{x}{x-3}$-$\frac{1}{2}$=$\frac{1}{2x-6}$
去分母,2x-(x-3)=1.
解这个方程,得x=-2.
检验:当x=-2时,2(x-3)≠0,所以x=-2是原方程的解.
∴原方程的解是x=-2.
点评 此题考查了解一元二次方程和解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解,解分式方程一定注意要验根.


 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:解答题
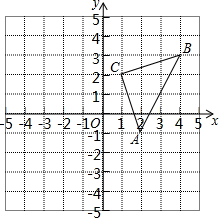 如图,平面直角坐标系中,△ABC的顶点都在网格点上,平移△ABC,使点B与坐标原点O重合,请在图中画出平移后的三角形A1OC1,并写出A1,C1的坐标.
如图,平面直角坐标系中,△ABC的顶点都在网格点上,平移△ABC,使点B与坐标原点O重合,请在图中画出平移后的三角形A1OC1,并写出A1,C1的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
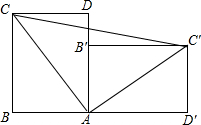 一个直立的火柴盒在桌面上倒下,启发人们发现了勾股定理的一种新的证法.如图,火柴盒的一个侧面ABCD倒下到AB′C′D′的位置,连接CC′,设AB=a.BC=b,AC=c,请利用四边形BCC′C的面积证明勾股定理.
一个直立的火柴盒在桌面上倒下,启发人们发现了勾股定理的一种新的证法.如图,火柴盒的一个侧面ABCD倒下到AB′C′D′的位置,连接CC′,设AB=a.BC=b,AC=c,请利用四边形BCC′C的面积证明勾股定理.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com