
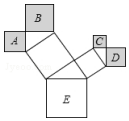
 如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C、E的面积分别为2,5,1,10.则正方形D的面积是2.
如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C、E的面积分别为2,5,1,10.则正方形D的面积是2. 科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=4x | B. | y=$\frac{1}{3x}$ | C. | y=$\frac{1}{{x}^{2}}$ | D. | y=$\frac{1}{x+1}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2017届湖北省襄阳市九年级下学期第一次月考数学试卷(解析版) 题型:解答题
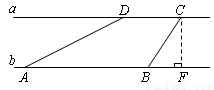
河流两岸a、b互相平行,C、D是河岸a上间隔50m的两个电线杆.某人在河岸b上的A处测得∠DAB=30°,然后沿河岸走了100m到达B处,测得∠CBF=60°,求河流的宽度CF的值(结果精确到个位).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com