
【题目】如图,有三张背面完全相同的纸牌A,B,C,其中正面分别画有三种不同的几何图形,小华将这3张纸牌背面朝上洗匀后摸出一张,放回洗匀后再摸出一张,请你用画树状图或列表的方法,求摸出的两张纸牌面上所画几何图形既是轴对称图形又是中心对称图形的概率. 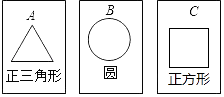
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,把直角△ABC的斜边AC放在定直线l上,按顺时针的方向在直线l上转动两次,使它转到△A2B1C2的位置,设AB= ![]() ,BC=1,则顶点A运动到点A2的位置时,点A所经过的路线为( )
,BC=1,则顶点A运动到点A2的位置时,点A所经过的路线为( ) 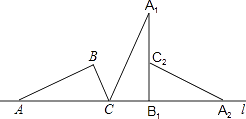
A.( ![]() +
+ ![]() )π
)π
B.( ![]() +
+ ![]() )π
)π
C.2π
D.![]() π
π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E分别是AB、AC的中点,下列说法中不正确的是( ) 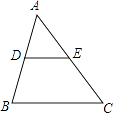
A.DE= ![]() BC
BC
B.![]()
C.△ADE∽△ABC
D.S△ADE:S△ABC=1:2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=10,点D是BC边上的一动点(不与B、C重合),∠ADE=∠B=∠α,DE交AB于点E,且tan∠α= ![]() ,有以下的结论:①△DBE∽△ACD;②△ADE∽△ACD;③△BDE为直角三角形时,BD为8或
,有以下的结论:①△DBE∽△ACD;②△ADE∽△ACD;③△BDE为直角三角形时,BD为8或 ![]() ;④0<BE≤5,其中正确的结论是(填入正确结论的序号)
;④0<BE≤5,其中正确的结论是(填入正确结论的序号) 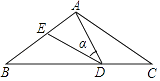
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,已知点A(﹣2,0),B(0,4),C(0,3),过点C作直线交x轴于点D,使得以D,O,C为顶点的三角形与△AOB相似,求点D的坐标. 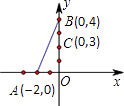
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,过点D作DE⊥AB于点E. 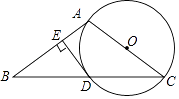
(1)求证:DE是⊙O的切线;
(2)若AC=10,BC=16,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
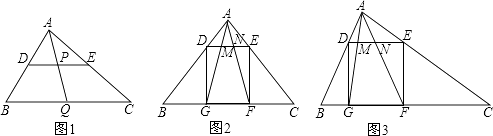
【题目】类比、转化、从特殊到一般等思想方法,在数学学习和研究中经常用到,如下是一个案例,请补充完整. 原题:如图1,在△ABC中,点D、E、Q分别在AB、AC、BC上,且DE∥BC,AQ交DE于点P,求证: ![]() .
.
(1)尝试探究:在图1中,由DP∥BQ得△ADP△ABQ(填“≌”或“∽”),则 ![]() = , 同理可得
= , 同理可得 ![]() =
= ![]() ,从而
,从而 ![]() .
.
(2)类比延伸:如图2,在△ABC中,∠BAC=90°,正方形DEFG的四个顶点在△ABC的边上,连接AG、AF分别交DE于M、N两点,若AB=AC=1,则MN的长为 .
(3)拓展迁移:如图3,在△ABC中,∠BAC=90°,正方形DEFG的四个顶点在△ABC的边上,连接AG、AF分别交于DE于M、N两点,AB<AC,求证:MN2=DMEN.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为( ) 
A.2 ![]()
B.8
C.2 ![]()
D.2 ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com