Question

【题目】在矩形中，点在边上，连接，．是线段上的定点，是线段上的动点，若，，，且周长的最小值为6，则的长为_______．

Answer 1

【答案】1．

【解析】

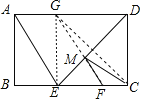
根据勾股定理得到BE==2，推出△CDE是等腰直角三角形，得到∠CDE=∠ADE=45°，作点C关于直线DE的对称点G，连接GF交DE于M，则DG=CD=4，此时，△MFC周长的最小值为6，设CF=x，则GF=6-x，连接GE，根据勾股定理列方程即可得到结论．

∵四边形ABCD是矩形，
∴∠B=90°，
∵AB=4，AE=2 ，
∴BE==2，
∵BC=AD=6，
∴CE=4，
∵CD=AB=4，∠DCE=90°，
∴△CDE是等腰直角三角形，
∴∠CDE=∠ADE=45°，
作点C关于直线DE的对称点G，连接GF交DE于M，
则DG=CD=4，此时，△MFC周长的最小值为6，
即CM+MF+CF=GM+MF+CF=GF+CF=6，
设CF=x，则GF=6-x，
连接GE，则GE⊥BC，EF=6-2-x，
在Rt△EGF中，EG2+EF2=GF2，
∴（4-x）2+42=（6-x）2，
解得：x=1，
∴CF=1，
故答案为：1．