
����Ŀ����ͼ����·![]() Ϊ���������ڵ�
Ϊ���������ڵ�![]() ��ƫ��
��ƫ��![]() �����ϣ�����
�����ϣ�����![]() ǧ�״��Ǵ�ׯ
ǧ�״��Ǵ�ׯ![]() ���ڵ�
���ڵ�![]() ��ƫ��
��ƫ��![]() �����ϣ�����
�����ϣ�����![]() ǧ�״��Ǵ�ׯ
ǧ�״��Ǵ�ׯ![]() ��Ҫ�ڹ�·
��Ҫ�ڹ�·![]() ����һ�����ز��չ�վ
����һ�����ز��չ�վ![]() (ȡ��
(ȡ��![]() ��
��![]() ��)��ʹ��
��)��ʹ��![]() ��
��![]() ����ׯ��
����ׯ��![]() վ�ľ���֮����̣�����ͼ������
վ�ľ���֮����̣�����ͼ������![]() ��λ�ã���д�����������㣺
��λ�ã���д�����������㣺
��1��![]() ��
��![]() ����ׯ֮��ľ��룻
����ׯ֮��ľ��룻
��2��![]() ��
��![]() ��
��![]() ����֮�͵���Сֵ.���ο����ݣ�sin36.5����0.6��cos36.5����0.8��tan36.5����0.75��������������.��
����֮�͵���Сֵ.���ο����ݣ�sin36.5����0.6��cos36.5����0.8��tan36.5����0.75��������������.��

���𰸡�(1) M��N����ׯ֮��ľ���Ϊ![]() ǧ��;(2) ��ׯM��N��Pվ����̾������5
ǧ��;(2) ��ׯM��N��Pվ����̾������5![]() ǧ�ף�
ǧ�ף�
��������
��1����N����AB�ĶԳƵ�N'��AB����E������MN����AB����P����PΪ���ز��չ�վ��λ�ã����DN��DM�����ù��ɶ������ɽ�����⣮
��2���������֪��M��N��AB�ϵ�P�ľ���֮����̳��Ⱦ���MN���ij���
�⣺��N����AB�ĶԳƵ�N'��AB����E������MN����AB����P����PΪ���ز��չ�վ��λ�ã�

��1����Rt��ANE��AN=10����NAB=36.5��
��NE=ANsin��NAB=10sin36.5��=6��
AE=ANcos��NAB=10cos36.5��=8��
��M��MC��AB�ڵ�C��
��Rt��MAC��AM=5����MAB=53.5��
��AC=MAsin��AMB=MAsin36.5��=3��
MC=MAcos��AMC=MAcos36.5��=4��
����M��MD��NE�ڵ�D��
��Rt��MND��MD=AE-AC=5��
ND=NE-MC=2��
��MN=![]() =
=![]() ��
��
��M��N����ׯ֮��ľ���Ϊ![]() ǧ�ף�
ǧ�ף�
��2���������֪��M��N��AB�ϵ�P�ľ���֮����̳��Ⱦ���MN���ij���
DN��=10��MD=5����Rt��MDN���У��ɹ��ɶ�������
MN��=![]() =5
=5![]() ��ǧ�ף�
��ǧ�ף�
���ׯM��N��Pվ����̾������5![]() ǧ�ף�
ǧ�ף�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η��̣�a+1��x2+2bx+��a+1����0��������ȵ�ʵ������������˵����ȷ���ǣ�������
A. 1һ�����Ƿ���x2+bx+a��0�ĸ�B. 0һ�����Ƿ���x2+bx+a��0�ĸ�
C. ��1�����Ƿ���x2+bx+a��0�ĸ�D. 1�ͩ�1���Ƿ���x2+bx+a��0�ĸ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ֽƬABC�У���A��90�㣬��C��30�㣬AC��10cm������ֽƬ�ع���B��ֱ���۵���ʹ��A����б��BC�ϵ�һ��E�����ۺۼ�ΪBD����ͼ1������ȥ��CDE��õ�˫���BDE����ͼ2���������Ź���BDEij�����ֱ�߽�˫�������μ�����ʹ��չ�����ƽ��ͼ������һ����ƽ���ı��Σ�������ƽ���ı��ε��ܳ�Ϊ_____cm��
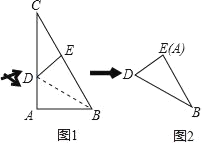
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ֱ��l��y=![]() x+m��x�ᡢy��ֱ��ڵ�A�͵�B��0����1����������y=
x+m��x�ᡢy��ֱ��ڵ�A�͵�B��0����1����������y=![]() x2+bx+c������B����ֱ��l����һ������ΪC��4��n����
x2+bx+c������B����ֱ��l����һ������ΪC��4��n����
��1����n��ֵ�������ߵĽ���ʽ��
��2����D���������ϣ�DE��y�ύֱ��l�ڵ�E����F��ֱ��l�ϣ����ı���DFEGΪ���Σ���ͼ2�������D�ĺ�����Ϊt��0��t��4��������DFEG���ܳ�Ϊp����p��t�ĺ�����ϵʽ�Լ�p�����ֵ��
��3������AOB��ƽ����ij��M��ת90���180�㣬�õ���A1O1B1����A��O��B�Ķ�Ӧ��ֱ��ǵ�A1��O1��B1������A1O1B1����������ǡ�������������ϣ���ô���Ǿͳ������ĵ�Ϊ����㡱����ֱ��д������㡱�ĸ�������ת180��ʱ��A1�ĺ����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��������OABC�ı�OC��OA�ֱ���x��y����������ϣ����B��4��4������P��t��0����x����һ���㣬����O��OH��AP�ڵ�H��ֱ��OH��ֱ��BC�ڵ�D����AD��
��1����ͼ1������P���߶�OC��ʱ����֤��OP��CD��
��2���ڵ�P�˶������У���AOP����A��B��DΪ���������������ʱ����t��ֵ��
��3����ͼ2��������y����![]() x2+
x2+![]() x+4���Ƿ���ڵ�Q��ʹ����P��D��Q��CΪ������ı���Ϊƽ���ı��Σ������ڣ������t��ֵ���������ڣ���˵�����ɣ�
x+4���Ƿ���ڵ�Q��ʹ����P��D��Q��CΪ������ı���Ϊƽ���ı��Σ������ڣ������t��ֵ���������ڣ���˵�����ɣ�
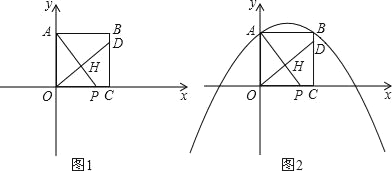
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������y=![]() ��x��0����ͼ����ֱ��AB���ڵ�A��2��3����ֱ��AB��x�ύ�ڵ�B��4��0��������B��x��Ĵ���BC����������������ͼ���ڵ�C����ƽ���ڴ��ڵ�D��ʹ����A��B��C��D�ĵ�Ϊ������ı���Ϊƽ���ı��Σ����D��������______��
��x��0����ͼ����ֱ��AB���ڵ�A��2��3����ֱ��AB��x�ύ�ڵ�B��4��0��������B��x��Ĵ���BC����������������ͼ���ڵ�C����ƽ���ڴ��ڵ�D��ʹ����A��B��C��D�ĵ�Ϊ������ı���Ϊƽ���ı��Σ����D��������______��
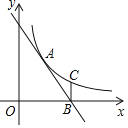
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������֣�
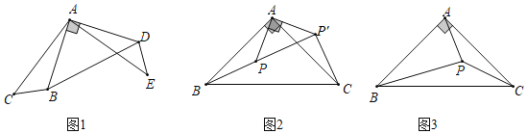
��1����ͼ1������ABC�Ƶ�A��ʱ����ת90���õ���ADE������BD�����ABD�Ķ�����______��
�����̽����
��2����ͼ2���ڵ���ֱ��������ABC��ȡһ��P��ʹ��APB=135��������ABP�ƶ���A��ʱ����ת90���õ���ACP'������PP'�������BP��CP'��������λ�ù�ϵ����˵�����ɣ�
��������⣩
��3����ͼ3���ڵ���ֱ��������ABC����ȡһ��P������PA��PB��PC����֤��PC+![]() PA��PB��
PA��PB��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
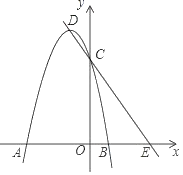
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y��ax2+2ax��3a��a��0����x���ཻ��A��B������y���ཻ�ڵ�C������ΪD��ֱ��DC��x���ཻ�ڵ�E��
��1����a����1ʱ�������߶���D������Ϊ�� ����OE���� ����
��2��OE�ij��Ƿ���aֵ�йأ�˵��������ɣ�
��3�����DEO������������30�����ӵ�60��Ĺ����У���D�˶���·������
��4����DEΪб�ߣ���ֱ��DE�����Ϸ�������Rt��PDE����P��m��n������ֱ��д��n����m�ĺ�������ʽ���Ա���m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������O�У�AB��ֱ����AD���ң���ADE = 60������C = 30����
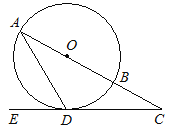
���ж�ֱ��CD�Ƿ�����O�����ߣ���˵�����ɣ�
����CD = ![]() ����BC�ij���
����BC�ij���
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com