

| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
分析 (1)根据四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点,可得EF=HG=$\frac{1}{2}$AC,EH=FG=$\frac{1}{2}$BD,进而得到中点四边形EFGH是平行四边形.
(2)连接AC,BD,判定△BPD≌△APC,即可得到AC=BD,据此可得EF=HG=$\frac{1}{2}$AC=EH=FG=$\frac{1}{2}$BD,即可得出中点四边形EFGH是菱形;
(3)根据∠APB=∠CPD=90°,可得AC⊥BD,进而得出EH⊥EF,即∠HEF=90°,据此可得菱形EFGH是正方形.
解答  解:如图①,连接AC,BD,
解:如图①,连接AC,BD,
∵点E、F、G、H分别为四边形ABCD的四边AB、BC、CD、DA的中点,
∴EF=HG=$\frac{1}{2}$AC,EH=FG=$\frac{1}{2}$BD,
∴四边形EFGH是平行四边形,故(1)正确;
如图②,连接AC,BD,
∵PA=PB,PC=PD,∠APB=∠CPD,
∴∠BPD=∠APC,
∴△BPD≌△APC,
∴AC=BD,
∵点E、F、G、H分别为四边形ABCD的四边AB、BC、CD、DA的中点,
∴EF=HG=$\frac{1}{2}$AC=EH=FG=$\frac{1}{2}$BD,
∴四边形EFGH是菱形,故(2)正确;
在(2)中增加条件∠APB=∠CPD=90°,其他条件不变,
由△BPD≌△APC,可得∠CAP=∠DBP,
∵△ABP中,∠PAB+∠ABD+∠DBP=90°,
∴∠PAB+∠ABD+∠CAP=90°,
∴AC⊥BD,
由点E、F、G、H分别为四边形ABCD的四边AB、BC、CD、DA的中点,可得EH∥BD,EF∥AC,
∴EH⊥EF,
即∠HEF=90°,
∴菱形EFGH是正方形,故(3)正确,
故选:D.
点评 本题考查的是中点四边形,三角形的中位线定理、菱形的判定、正方形的判定.解题时注意:一般中点四边形是平行四边形;如果对角线相等,则得到的中点四边形是菱形,如果对角线互相垂直,则得到的中点四边形是矩形,如果对角线相等且互相垂直,则得到的中点四边形是正方形.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小李从甲地前往乙地,到达乙地休息了半个小时后,又按原路返回甲地,他与甲地的距离y(千米)和所用的时间x(小时)之间的函数关系如图所示.
小李从甲地前往乙地,到达乙地休息了半个小时后,又按原路返回甲地,他与甲地的距离y(千米)和所用的时间x(小时)之间的函数关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
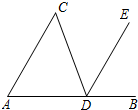 如图,点B是△ADC的边AD的延长线上一点,DE∥AC,若∠C=50°,∠A=60°,则∠CDB的度数等于( )
如图,点B是△ADC的边AD的延长线上一点,DE∥AC,若∠C=50°,∠A=60°,则∠CDB的度数等于( )| A. | 70° | B. | 100° | C. | 110° | D. | 120° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为30海里的A处,轮船沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,则此时轮船所在位置B处于灯塔P之间的距离为30$\sqrt{3}$海里.
如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为30海里的A处,轮船沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,则此时轮船所在位置B处于灯塔P之间的距离为30$\sqrt{3}$海里.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com