
【题目】已知函数 ![]() 是关于x的二次函数,求:
是关于x的二次函数,求:
(1)满足条件的m的值;
(2)m为何值时,抛物线有最低点?求出这个最低点,当x为何值时,y随x的增大而增大;
(3)m为何值时,抛物线有最大值?最大值是多少?当x为何值时,y随x的增大而减小?
科目:初中数学 来源: 题型:
【题目】如图,函数y=![]() 和y= - x+4的图像交点为A、B,原点为O,求△AOB面积.
和y= - x+4的图像交点为A、B,原点为O,求△AOB面积.

【答案】8![]()
【解析】整体分析:
联立方程y=![]() 和y= - x+4,求出点A,B的坐标,然后由公式△OAB的面积=
和y= - x+4,求出点A,B的坐标,然后由公式△OAB的面积=![]() ×(x1- x2)(y2- y1)求解.
×(x1- x2)(y2- y1)求解.
解:把y=![]() 代入y= - x+4得,
代入y= - x+4得,
![]() = - x+4,
= - x+4,
解得x1=2+![]() ,x2=2-
,x2=2-![]() .
.
所以y1=2-![]() ,y2=2+
,y2=2+![]() .
.
则A(2-![]() ,2+
,2+![]() ),B(2+
),B(2+![]() ,2-
,2-![]() ),
),
所以△OAB的面积=![]() ×(x1- x2)(y2- y1)==
×(x1- x2)(y2- y1)==![]() ×4
×4![]() ×4
×4![]() =
=![]() .
.
【题型】解答题
【结束】
19
【题目】如图,直线![]() 与双曲线
与双曲线![]() 相交于A(2,1)、B两点.
相交于A(2,1)、B两点.

(1)求m及k的值;
(2)不解关于x、y的方程组 直接写出点B的坐标;
直接写出点B的坐标;
(3)直线![]() 经过点B吗?请说明理由.
经过点B吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
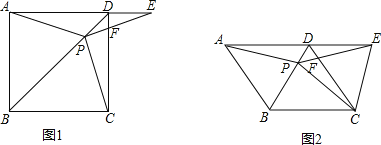
【题目】如图1在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.
(1)证明:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120度时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法错误的是( )
A.在二次函数 ![]() 中,当
中,当 ![]() 时,
时, ![]() 随
随 ![]() 的增大而增大
的增大而增大
B.在二次函数 ![]() 中,当
中,当 ![]() 时,
时, ![]() 有最大值
有最大值 ![]()
C.![]() 越大图象开口越小,
越大图象开口越小, ![]() 越小图象开口越大
越小图象开口越大
D.无论 ![]() 是正数或负数,
是正数或负数, ![]()
![]() 的顶点一定是坐标原点
的顶点一定是坐标原点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( ).
A. m=-2是方程m-2=0的解 B. m=6是方程3m+18=0的解
C. x=-1是方程-![]() =0的解 D. x=
=0的解 D. x=![]() 是方程10x=1的解
是方程10x=1的解
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=mx﹣3m2+12,请按要求解答问题:
(1)m为何值时,函数图象过原点,且y随x的增大而减小?
(2)若函数图象平行于直线y=﹣x,求一次函数解析式;
(3)若点(0,﹣15)在函数图象上,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某市九年级学生学业考试体育成绩,现从中随机抽取部分学生的体育成绩进行分段(A:50分; B:49-45分;C:44-40分;D:39-30分;E:29-0分).每段包含最高分,不包含最低分,统计表如下,统计图如图所示.
分数段 | 频数(人) | 百分比 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

根据上面提供的信息,回答下列问题:
(1)在统计表中,![]() 的值为___,
的值为___, ![]() 的值为__,并将统计图补充完整.
的值为__,并将统计图补充完整.
(2)成绩在40分以上定为优秀,那么该市今年10440名九年级学生中体育成绩为优秀的学生约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农场拟建三件矩形饲养室,饲养室一面靠现有墙(墙可用长≤20m),中间用两道墙隔开,已知计划中的建筑材料可建围墙的总长为60m,设饲养室宽为x(m),总占地面积为y(m2)(如图所示). 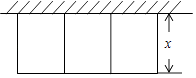
(1)求y关于x的函数表达式,并直接写出自变量x的取值范围;
(2)三间饲养室占地总面积有可能达到210m2吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com