
| 甲 | 16 | 18 | 18 | 19 | 20 | 20 | 21 | 21 | 23 | 24 |
| 乙 | 13 | 15 | 17 | 18 | 20 | 21 | 23 | 23 | 24 | 26 |
分析 (1)根据平均数的计算公式分别进行计算即可得出答案;
(2)根据方差公式S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2],分别进行计算,再根据方差的意义即可得出答案;
解答 解:(1)甲的平均数是:
(16+18+18+19+20+20+21+21+23+24)÷10=20(cm),
乙的平均数是:
(13+15+17+18+20+21+23+23+24+26)÷10=20(cm);
(2)${S}_{甲}^{2}$=$\frac{1}{10}$[(16-20)2+(18-20)2+(18-20)2+(19-20)2+(20-20)2+(20-20)2+(21-20)2+(21-20)2+(23-20)2+(24-20)2]=5.2(cm2);
${S}_{乙}^{2}$=$\frac{1}{10}$[(13-20)2+(15-20)2+(17-20)2+(18-20)2+(20-20)2+(21-20)2+(23-20)2+(23-20)2+(24-20)2+(26-20)2]=15.8(cm2);
因为${S}_{甲}^{2}$<${S}_{乙}^{2}$,所以甲种小麦长得比较整齐.
点评 此题考查了平均数和方差,一般地设n个数据,x1,x2,…xn的平均数为$\overline{x}$,则方差S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.


科目:初中数学 来源: 题型:解答题
 小明的奶奶每天晚饭后从家中出发去散步,她所出门的时间与离家距离之间的关系如图.
小明的奶奶每天晚饭后从家中出发去散步,她所出门的时间与离家距离之间的关系如图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
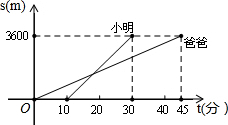 星期天,小明和爸爸去大剧院看电影.爸爸步行先走,小明在爸爸离开家一段时间后骑自行车去,两人按相同的路线前往大剧院,他们所走的路程s(米)和时间t(分)的关系如图所示.则小明追上爸爸时,爸爸共走了( )
星期天,小明和爸爸去大剧院看电影.爸爸步行先走,小明在爸爸离开家一段时间后骑自行车去,两人按相同的路线前往大剧院,他们所走的路程s(米)和时间t(分)的关系如图所示.则小明追上爸爸时,爸爸共走了( )| A. | 12分钟 | B. | 15分钟 | C. | 18分钟 | D. | 21分钟 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 甲乙两城市相距600千米,一辆货车和一辆客车均从甲城市出发匀速行驶至乙城市.已知货车出发1小时后客车再出发,先到终点的车辆原地休息.在汽车行驶过程中,设两车之间的距离为s(千米),客车出发的时间为t(小时),它们之间的关系如图所示,则下列结论错误的是( )
甲乙两城市相距600千米,一辆货车和一辆客车均从甲城市出发匀速行驶至乙城市.已知货车出发1小时后客车再出发,先到终点的车辆原地休息.在汽车行驶过程中,设两车之间的距离为s(千米),客车出发的时间为t(小时),它们之间的关系如图所示,则下列结论错误的是( )| A. | 货车的速度是60千米/小时 | |
| B. | 离开出发地后,两车第一次相遇时,距离出发地150千米 | |
| C. | 货车从出发地到终点共用时7小时 | |
| D. | 客车到达终点时,两车相距180千米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
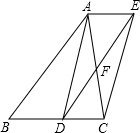 如图,已知点D是△ABC的边BC的中点,直线AE∥BC,过点D作直线DE∥AB,分别交AE、AC于点E、F.
如图,已知点D是△ABC的边BC的中点,直线AE∥BC,过点D作直线DE∥AB,分别交AE、AC于点E、F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com