
【题目】为了解决农民工子女入学难的问题,我市建立了一套进城农民工子女就学的保障机制,其中一项就是免交“借读费”.据统计,2004年秋季有![]() 名农民工子女进入主城区中小学学习,预计2005年秋季进入主城区中小学学习的农民工子女比2004年有所增加,其中小学增加
名农民工子女进入主城区中小学学习,预计2005年秋季进入主城区中小学学习的农民工子女比2004年有所增加,其中小学增加![]() ,中学增加
,中学增加![]() ,这样,2005年秋季将新增
,这样,2005年秋季将新增![]() 名农民工子女在主城区中小学学习.
名农民工子女在主城区中小学学习.
(1)如果按小学每生每年收“借读费”![]() 元,中学每生每年收“借读费”
元,中学每生每年收“借读费”![]() 元计算,求2005年新增加的
元计算,求2005年新增加的![]() 名中小学学生共免收多少“借读费”?
名中小学学生共免收多少“借读费”?
(2)如果小学每增加![]() 名学生需配备
名学生需配备![]() 名教师,中学每增加
名教师,中学每增加![]() 名学生需配备
名学生需配备![]() 名教师,若按2005年秋季入学后,农民工子女在主城区中小学就读的学生增加的人数计算,一共需要配备多少名中小学教师?
名教师,若按2005年秋季入学后,农民工子女在主城区中小学就读的学生增加的人数计算,一共需要配备多少名中小学教师?
【答案】(1)820000元;(2)480人.
【解析】
本题考查的是方程组的应用
(1)根据题意可知本题的等量关系有,2005年进入小学学习的人数=(1+20%)×2004年进入小学学习的人数,2005年进入中学学习的人数=(1+30%)×2004进入中学学习的人数.2005年进入中小学学习的总人数=5000+1160.依此列方程组再求解.
(2)先算出秋季入学后,在小学就读的学生人数及在中学就读的学生人数,再根据师生比例即得结果。
(1)设2004年秋季在主城区小学学习的农民工子女有![]() 人,在主城区中学学习的农民工子女有
人,在主城区中学学习的农民工子女有![]() 人,由题意可得:
人,由题意可得:
![]()
解得![]()
∴![]() ,
,![]()
∴500×680+1000×480=820000(元)=82(万元)
答:共免收82万元(或820000元)“借读费”.
(2)2005年秋季入学后,在小学就读的学生有![]() (名),在中学就读的学生
(名),在中学就读的学生
有![]() (名).
(名).
∴![]() (名)
(名)
答:一共需要配备360名中小学教师.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某班将买一些乒乓球和乒乓球拍.了解信息如下:甲、乙两家商店出售两种同样品牌的乒乓球和乒乓球拍.乒乓球拍每副定价30元,乒乓球每盒定价5元;经洽谈:甲店每买一副球拍赠一盒乒乓球;乙店全部按定价的9折优惠.该班需球拍5副,乒乓球若干盒(不小于5盒).问:
(1)当购买乒乓球x盒时,两种优惠办法各应付款多少元?(用含x的代数式表示)
(2)如果要购买15盒乒乓球时,请你去办这件事,你打算去哪家商店购买?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC是等边三角形,D是BC边上的一个动点(点D不与B,C重合)△ADF是以AD为边的等边三角形,过点F作BC的平行线交射线AC于点E,连接BF.

(1)如图1,求证:△AFB≌△ADC;
(2)请判断图1中四边形BCEF的形状,并说明理由;
(3)若D点在BC 边的延长线上,如图2,其它条件不变,请问(2)中结论还成立吗?如果成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰直角三角形,AC=BC=a,以斜边AB上的点O为圆心的圆分别与AC,BC相切于点E,F,与AB分别交于点G,H,且EH的延长线和CB的延长线交于点D,则CD的长为 . 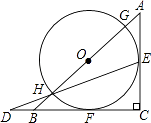
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,定点E,F分别在直线AB,CD上,在平行线AB、CD之间有一动点P,满足0°<∠EPF<180°.


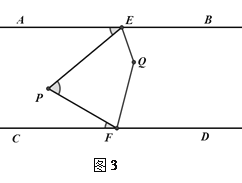

(1)试问∠AEP,∠EPF,∠PFC满足怎样的数量关系?
解:由于点P是平行线AB、CD之间有一动点,因此需要对点P的位置进行分类讨论;如图1,当P点在EF的左侧时,∠AEP,∠EPF,∠PFC满足数量关系为______________,如图2,当P点在EF的右侧时,∠AEP,∠EPF,∠PFC满足数量关系为______________。
(2)如图3,QE,QF分别平分∠PEB和∠PFD,且点P在EF左侧.
①若∠EPF=60°,则∠EQF=_______°.
②猜想∠EPF与∠EQF的数量关系,并说明理由.
③如图4,若∠BEQ与∠DFQ的角平分线交于点Q1,∠BEQ1与∠DFQ1的角平分线交于点Q2,∠BEQ2与∠DFQ2的角平分线交于点Q3,此次类推,则∠EPF与∠EQ2018F满足怎样的数量关系?(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,点P是CD的中点,∠BCD=60°,射线AP交BC的延长线于点E,射线BP交DE于点K,点O是线段BK的中点,作BM⊥AE于点M,作KN⊥AE于点N,连结MO、NO,以下四个结论:①△OMN是等腰三角形;②tan∠OMN= ![]() ;③BP=4PK;④PMPA=3PD2 , 其中正确的是( )
;③BP=4PK;④PMPA=3PD2 , 其中正确的是( )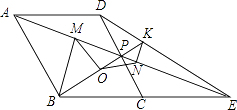
A.①②③
B.①②④
C.①③④
D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线. 
(1)如图1,在△ABC中,CD为角平分线,∠A=40°,∠B=60°,求证:CD为△ABC的完美分割线.
(2)在△ABC中,∠A=48°,CD是△ABC的完美分割线,且△ACD为等腰三角形,求∠ACB的度数.
(3)如图2,△ABC中,AC=2,BC= ![]() ,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从汽车灯的点O处发出的一束光线经灯的反光罩反射后沿CO方向平行射出,如入射光线OA的反射光线为AB,∠OAB=75°.在如图中所示的截面内,若入射光线OD经反光罩反射后沿DE射出,且∠ODE=22°.则∠AOD的度数是_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com