
【题目】关于x的一元二次方程x2﹣2x+m﹣1=0有两个实数根,则m的取值范围是_____.
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c交x轴于A、B两点,交y轴于点C,已知抛物线的对称轴为x=1,B(3,0),C(0,-3),
(1)求二次函数y=ax2+bx+c的解析式;
(2)在抛物线对称轴上是否存在一点P,使点P到B、C两点距离之差最大?若存在,求出P点坐标;若不存在,请说明理由;
(3)平行于x轴的一条直线交抛物线于M,N两点,若以MN为直径的圆恰好与x轴相切,求此圆的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
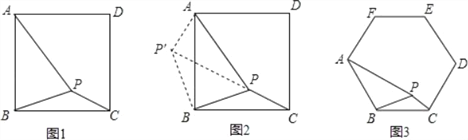
【题目】如图1,在正方形ABCD内有一点P,PA=3,PB=2,PC=1,求∠BPC的度数.
分析:根据已知条件比较分散的特点,我们可以通过旋转变换将分散的已知条件集中在一起,于是将△BPC绕点B逆时针旋转90°,得到了△BP′A(如图2),然后连结PP′,这时再分别求出∠BP′P和∠AP′P的度数.
解答:(1)请你根据以上分析再通过计算求出图2中∠BPC的度数;
(2)如图3,若在正六边形ABCDEF内有一点P,且PA=2![]() ,PB=4,PC=2,求∠BPC的度数.
,PB=4,PC=2,求∠BPC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AOB是一条直线,OC是∠AOD的平分线,OE 是∠BOD的平分线.
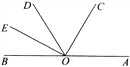
(1)若∠AOE=140°,求∠AOC的度数;
(2)若∠EOD :∠COD=2 : 3,求∠COD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①是一面矩形彩旗完全展平时的尺寸图(单位:cm),其中矩形ABCD是由双层白布缝制的穿旗杆用的旗裤,阴影部分DCEF为矩形绸缎旗面. 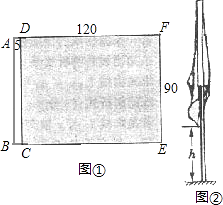
(1)用经加工的圆木杆穿入旗裤作旗杆,求旗杆的最大直径(精确到1cm);
(2)将穿好彩旗的旗杆垂直插在操场上,旗杆从旗顶到地面的高度为220cm,在无风的天气里,彩旗自然下垂,如图②,求彩旗下垂时最低处离地面的最小高度h.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=ax2+bx+5的图象过A(﹣1,0),B(5,0)两点,与y轴交于点C,作直线BC,动点P从点C出发,以每秒![]() 个单位长度的速度沿CB向点B运动,运动时间为t秒,当点P与点B重合时停止运动.
个单位长度的速度沿CB向点B运动,运动时间为t秒,当点P与点B重合时停止运动.
(1)求抛物线的表达式;
(2)如图2,当t=1时,若点Q是X轴上的一个动点,如果以Q,P,B为顶点的三角形与△ABC相似,求出Q点的坐标;
(3)如图3,过点P向x轴作垂线分别交x轴,抛物线于E、F两点.
①求PF的长度关于t的函数表达式,并求出PF的长度的最大值;
②连接BF,将△PBF沿BF折叠得到△P′BF,当t为何值时,四边形PFP′B是菱形?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com