
【题目】铜梁永辉商场今年二月份以每桶40元的单价购进1000桶甲、乙两种食用油,然后以甲种食用油每桶75元、乙桶食用油每桶60元的价格售完,共获利29000元.
(1)求该商场分别购进甲、乙两种食用油多少桶?
(2)为了增加销售量,获得最大利润,根据销售情况和市场分析,在进价不变的情况下该经销商决定调整价格,将甲种食用油的价格在二月份的基础上下调20%,乙种食用油的价格上涨![]() a%,但甲的销售量还是较二月下降了
a%,但甲的销售量还是较二月下降了![]() a%,而乙的销售量却上升了25%,结果三月份的销售额比二月份增加了1000元,求a的值.
a%,而乙的销售量却上升了25%,结果三月份的销售额比二月份增加了1000元,求a的值.
科目:初中数学 来源: 题型:
【题目】2015年12月16日,南京大报恩寺遗址公园正式对外开放.某校数学兴趣小组想测量大报恩塔的高度.如图,成员小明利用测角仪在B处测得塔顶的仰角α=63.5°,然后沿着正对该塔的方向前进了13.1m到达E处,再次测得塔顶的仰角β=71.6°.测角仪BD的高度为1.4m,那么该塔AC的高度是多少?(参考数据:sin63.5°≈0.90,cos63.5°≈0.45,tan63.5°≈2.00,sin71.6°≈0.95,cos71.6°≈0.30,tan71.6°≈3.00)


查看答案和解析>>
科目:初中数学 来源: 题型:
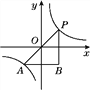
【题目】反比例函数y=![]() 的图象如图所示,A,P为该图象上的点,且关于原点成中心对称.在△PAB中,PB∥y轴,AB∥x轴,PB与AB相交于点B.若△PAB的面积大于12,则关于x的方程(a-1)x2-x+
的图象如图所示,A,P为该图象上的点,且关于原点成中心对称.在△PAB中,PB∥y轴,AB∥x轴,PB与AB相交于点B.若△PAB的面积大于12,则关于x的方程(a-1)x2-x+![]() =0的根的情况是________________.
=0的根的情况是________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学需要刻录一批电脑光盘,若到电脑公司刻录,每张需8元(包括空白光盘费);若学校自刻,出租用刻录机需120元外,每张光盘还需成本4元(包括空白光盘费)。问刻录这批电脑光盘,该校如何选择,才能使费用较少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,EF⊥AC于点F,DB⊥AC于点M,∠1=∠2,∠3=∠C,请问AB与MN平行吗?说明理由.完成下列推理过程:

解:AB∥MN.理由如下:
∵EF⊥AC,DB⊥AC,(已知),
∴∠CFE=∠CMD=90°,( )
∴EF∥DM,( )
∴∠2=∠CDM,( )
∵∠1=∠2,(已知),
∴∠1=∠ ( )
∴MN∥CD,( )
∵∠3=∠C,(已知),
∴AB∥CD,( ),
∴AB∥MN.( )
查看答案和解析>>
科目:初中数学 来源: 题型:
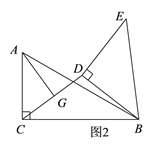
【题目】如图1,两块直角三角纸板(Rt△ABC和Rt△BDE)按图所示的方式摆放(重合点为B),其中∠BDE=∠ACB=90°,∠ABC=30°,BD=DE=AC=2.将△BDE绕着点B顺时针旋转.
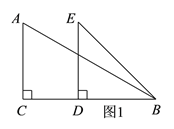
(1)当点D在BC上时,求CD的长;
(2)当△BDE旋转到A,D,E三点共线时,求△CDE的面积;
(3)如图2,连接CD,点G是CD的中点,连接AG,求AG的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成。硬纸板以如图两种方式裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面; B方法:剪4个侧面和5个底面。

现有19张硬纸板,裁剪时![]() 张用A方法,其余用B方法。
张用A方法,其余用B方法。
(1)用![]() 的代数式分别表示裁剪出的侧面和底面的个数;
的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在Rt△ABC,∠ACB=90°,分别以AB、BC为一边向外作正方形ABFG、BCED,连结AD、CF,AD与CF交于点M;
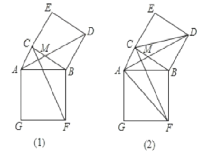
(1)求证:△ABD≌△FBC;
(2) 如图(2),已知AD=6,求四边形AFDC的面积;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com