
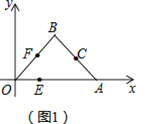
����Ŀ����֪���磨ͼ1������ƽ��ֱ�������У�A(12��0)��B(6��6)����CΪ�߶�AB���е㣬��D��ԭ��O���ڵ�C�Գƣ�
��1������ֱ�ߺ�Բ���ڣ�ͼ1����������D��λ�ã�������ͼ�ۼ������ж��ı���OBDA����״����˵�����ɣ�
��2���ڣ�ͼ1���У�����E�ӵ�O��������ÿ��1����λ���ٶ����߶�OA�˶��������Aʱֹͣ��ͬʱ������F�ӵ�O��������ÿ��a����λ���ٶ���OB��BD��DA�˶��������Aʱֹͣ�����˶���ʱ��Ϊt���룩��
�ٵ�t=4ʱ��ֱ��EFǡ��ƽ���ı���OBDA���������a��ֵ��
�ڵ�t=5ʱ��CE=CF����ֱ��д��a��ֵ��
���𰸡���1���ı���OBDA��ƽ���ı��Σ�����������2����2+![]() ����
����![]() ��
��![]() ��
��![]()
��������
��1��������OC����ȡCD=OC��Ȼ���ɶԽ�����ƽ�ֵ��ı�����ƽ���ı��ν��пɵõ��ı��ε���״��
��2������ֱ��EFǡ��ƽ���ı���OBDA�������ֱ֪��EF�ع�C����������֤����OEC�ա�DFC���Ӷ������DF�ij��ȣ����ǵõ�BF=8��Ȼ�����������ľ��빫ʽ���OB�ij����Ӷ������a��ֵ��
������õ�E�����꣬Ȼ�����EC�ij����Ӷ��õ�CF1�ij���Ȼ�����ݹ��ɶ������涨��֤����OBA=90��������BCF1�У����ݹ��ɶ��������BF1�ij����Ӷ������a��ֵ�����F2�����꣨b��6������CE=CF�г�����b�ķ��̿���õ�F2�����꣬�Ӷ������a��ֵ����Rt��CAF3�У�ȡ��AF3�ij����Ӷ���õ�F�˶���·�̣����ǿ����a��ֵ��
�⣺��1����ͼ��ʾ��
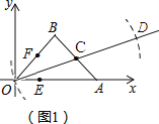
�ı���OBDA��ƽ���ı��Σ�
�������£��ߵ�CΪ�߶�AB���е㣬
��CB=CA��
�ߵ�D��ԭ��O���ڵ�C�Գƣ�
��CO=CD��
���ı���OBDA��ƽ���ı��Σ�
��2������ͼ2��ʾ��
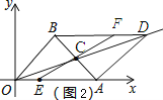
��ֱ��EFǡ��ƽ���ı���OBDA�������
��ֱ��EF�ع�C��9��3����
��t=4��
��OE=4��
��BD��OA��
���COE=��CDF��
������OEC����DFC�� ��
��
���OEC�ա�DFC��
��DF=OE=4��
��BF=12-4=8��
�������ľ��빫ʽ��֪OB=![]() =6
=6![]() ��
��
��4a=6![]() +8��
+8��
��a=2+![]() ��
��
����ͼ3��ʾ��
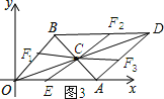
�ߵ�t=5ʱ��OE=5��
���E�����꣨5��0����
�������ľ��빫ʽ��֪EC=![]() =5��
=5��
��CE=CF��
��CF=5��
�������ľ��빫ʽ��֪OB=BA=6![]() ��
��
�֡�OA=12��
���OBAΪֱ�������Σ�
���OBA=90����
����ֱ����F1BC�У�CF1=5��BC=3![]() ��
��
��BF1=![]() ��
��
��OF1=6![]() -
-![]() ��
��
��a=![]() ��
��
����F2������Ϊ��b��6�����������ľ��빫ʽ��֪![]() =5��
=5��
��ã�b=5����ȥ����b=13��
��BF2=13-6=7��
��OB+BF2=6![]() +7��
+7��
��a=![]() ��
��
�ۡ�BO��AD��
���BAD=��OBA=90����
��AF3=![]() =
=![]() ��
��
��DF3=6![]() -
-![]() ��
��
��OB+BD+DF3=6![]() +12+6
+12+6![]() -
-![]() =12
=12![]() -
-![]() +12��
+12��
��a=![]() ��
��
��������a��ֵΪ![]() ��
��![]() ��
��![]() ��
��


 ���ݼ���ϵ�д�
���ݼ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ͬʱ��ʼ�ӹ�һ����װ���ӿ�ʼ�ӹ������������װ�׳��乤����8Сʱ���ҳ�������;ͣ��һ��ʱ��ά���豸��Ȼ���ڼ׳���ӹ���4Сʱʱ��ͣ��ǰ�Ĺ���Ч�ʼ����ӹ���ֱ����׳���ͬʱ���������װ�ļӹ�������ס�����������Լӹ���װ������Ϊ![]() ���������׳���ӹ���ʱ��Ϊ
���������׳���ӹ���ʱ��Ϊ![]() ��ʱ����
��ʱ����![]() ��
��![]() �ĺ���ͼ����ͼ��ʾ��
�ĺ���ͼ����ͼ��ʾ��
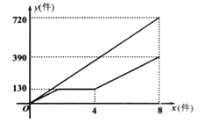
��1���׳���ÿСʱ�ӹ���װ�ļ���Ϊ________����������װ���ܼ���Ϊ________����
��2���ҳ��仨�˶���ʱ��ά���豸��
��3����ס�������������������£���ͬ��ɼӹ�800����װʱ�׳������õ�ʱ�䣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijһ���̶ӣ��ڹ����б�ʱ���ӵ��ס����������̶ӵ�Ͷ���飬ʩ��һ�죬�踶���̶ӹ��̿�1.2��Ԫ���ҹ��̶ӹ��̿�0.5��Ԫ�� �����쵼С����ݼס������ӵ�Ͷ������㣬�����·�����
��1���ӵ����������̸պ�������ɣ�
��2���Ҷӵ�����������Ҫ�ȹ涨���ڶ���6�죻
��3�����ס������Ӻ���3�죬���µĹ������Ҷӵ�����Ҳ����������ɣ�
���ʣ��ڲ������ڵ�ǰ���£��������һ��ʩ���������ʡ���̿��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
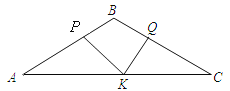
����Ŀ����ͼ������ABC�У�AB��BC��4��S��ABC��4![]() ����P��Q��K�ֱ�Ϊ�߶�AB��BC��AC������һ�㣬��PK��QK����СֵΪ_______
����P��Q��K�ֱ�Ϊ�߶�AB��BC��AC������һ�㣬��PK��QK����СֵΪ_______
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
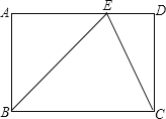
����Ŀ����ͼ���ھ���ABCD�У���E��AD�ϣ���ECƽ�֡�BED��
��1����BEC�Ƿ�Ϊ���������Σ�֤����Ľ��ۣ�
��2����AB=2����DCE=22.5������BC����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ת����ת�̱���������ֱ���ֳ����ĸ��ֱ�������ֵ������������б���������1��������Բ�Ľ�Ϊ120����ת��ת�̣���ת���Զ�ֹͣ��ָ��ָ��һ�����ε��ڲ�����������ڵ����ּ�Ϊת�������֣���ʱ����Ϊת��ת��һ�Σ���ָ��ָ���������εĽ��ߣ���ת���Ĵ���������ת��ת�̣�ֱ��ָ��ָ��һ�����ε��ڲ�Ϊֹ��
(1)ת��ת��һ�Σ���ת���������ǣ�2�ĸ��ʣ�
(2)ת��ת�����Σ�����״ͼ���б����������ηֱ�ת��������֮��Ϊ�����ĸ��ʣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=ax2+bx+c��a��0���IJ���ͼ����ͼ��ͼ����㣨��1��0�����Գ���Ϊֱ��x=2�����н��ۣ�
��4a+b=0����9a+c��3b����8a+7b+2c��0������x����1ʱ��y��ֵ��xֵ�������������������ֵy<0ʱ���Ա���x��ȡֵ��Χ��x<-1��x>5.
������ȷ�Ľ����У�������

A. 2�� B. 3�� C. 4�� D. 5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ֱ��y= ![]() x+2��x�ᣬy��ֱ��ཻ��A��B���㣬�뷴��������y=
x+2��x�ᣬy��ֱ��ཻ��A��B���㣬�뷴��������y= ![]() ��x��0����ͼ���ཻ�ڵ�C��2��3������P�Ƿ���������ͼ����һ�㣬��PE��ֱx����E������P��O��EΪ���������������AOB���ƣ����P��������________��
��x��0����ͼ���ཻ�ڵ�C��2��3������P�Ƿ���������ͼ����һ�㣬��PE��ֱx����E������P��O��EΪ���������������AOB���ƣ����P��������________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ������AB��25�ף���ͼ����б����һ��ǽAC�ϣ���ʱ���ݵ�B��ǽ��C�ľ���BCΪ7�ף�
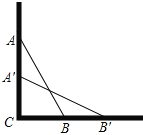
��1�������ݵĶ��˾����AC�ж�ߣ�
��2��������ݵĶ���A�»���4�ף���ô���ĵײ�B��ˮƽ�������һ����˶����ף�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com