Question

16．如图，将边长为6的正方形ABCD绕点A顺时针旋转，得到正方形AMNP，当点P第一次落在AC上时，正方形停止旋转，在旋转过程中，MN交直线AB于点E，PN交AC于点F．
（1）连接DP，BM，CN，如果DP=m，则BM=m，CN=$\sqrt{2}$m；（用含m的代数式表示）；
（2）连接MP，EF，当EF∥MP时，求正方形ABCD旋转的角度；
（3）在正方形ABCD旋转过程中，且点P在△ACD内部时，△NEF的周长是否发生变化？如果不变，求出△NEF的周长；如果变化，说明变化情况及理由．

Answer 1

分析 （1）由正方形的性质和旋转的特点，判断出△DAP≌△BAM和△DAP∽△CAN，利用勾股定理，计算即可；
（2）由正方形的性质和旋转角不变，得到∠PAF=∠FAN=∠NAE=∠MAE，而这四个角的和为90°得到旋转角为22.5°；
（3）由正方形的性质和旋转的特点，判断出△DAG≌△MAE，△CKF≌△NKI，△ADH≌△ABI，△AHG≌△AIG得到线段的转化．

解答 解：（1）如图1，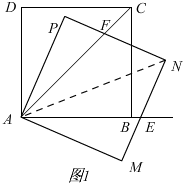

由旋转有，∠DAP=∠BAM，AD=AP，AB=AM，
∵正方形ABCD绕点A顺时针旋转，得到正方形AMNP，
∴AD=AP=AB=AM，
在△DAP和△BAM中
$\left\{\begin{array}{l}{AD=AB}\\{∠DAP=∠BAM}\\{AP=AM}\end{array}\right.$，
∴△DAP≌△BAM，
∴DP=BM=m，
∵AC为正方形ABCD的对角线，
∴AC=6$\sqrt{2}$，
连接AN，由旋转有，AD=AP=6，AC=AN=6$\sqrt{2}$，∠DAP=∠CAN，
∴△DAP∽△CAN，
∴$\frac{DP}{CN}=\frac{AD}{AC}$=$\frac{6}{6\sqrt{2}}$，
∴CN=$\sqrt{2}$DP=$\sqrt{2}$m，
故答案为m，$\sqrt{2}$m；
（2）连接PM，EF，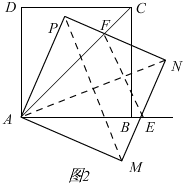

∵AN，PM是正方形APNM的对角线，
∴AN⊥PM，∠ANP=∠ANM=45°，
∵EF∥MP，
∴EF⊥AN，
∵∠ANP=∠ANM=45°，
∴AF=AE，
∵∠APF=∠AME=90°，AP=AM
∴△APF≌△AME，
∴∠PAF=∠MAE，
∵∠PAF+∠NAF=∠MAE+∠NAE=45°，
∴∠NAF=∠NAE，
由旋转有，∠NAF=∠MAE，
∴∠PAF=∠FAN=∠NAE=∠MAE，
∵∠PAM=90°，
∴∠PAF+∠FAN+∠NAE+∠MAE=90°，
∴∠MAE=$\frac{1}{4}$×90°=22.5°，
即：当EF∥MP时，正方形ABCD旋转的角度为22.5°；
（3）在正方形ABCD旋转过程中，且点P在△ACD内部时，△NEF的周长不发生变化，△NEF的周长为12；
如图3，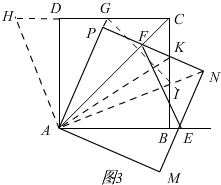

延长AP交C于G，连接AN交BC于I，
∵四边形ABCD，APNM都为正方形，
∴AD=AM，∠ADG=∠AME，
由旋转有，∠DAG=∠MAE，
∴△DAG≌△MAE，
∴DG=ME，
∵CG=CD-DG，NE=MN-ME，
∴CG=NE，
由旋转有，PK=BK，
∵CK=BC-BK，NK=PN-PK，
∴CK=NK，
∵∠FCK=∠INK=45°，∠CKF=∠NKI，
∴△CKF≌△NKI，
∴KF=KI，
∵CK=NK，
∴NF=CI，
∵EF²=NF²+NE²=CI²+CG²=GI²，
∴EF=GI，
延长CD到H，使DH=BI，
∵∠ADH=∠ABI，AD=AB，
∴△ADH≌△ABI，
∴∠DAH=∠BAI，
由旋转有，∠DAG=∠CAN，
∵∠DAC=∠BAC=45°，
∴∠GAF=∠BAI，
∴∠HAG=∠IAG，
∵AH=AI，AG=AG，
∴△AHG≌△AIG，
∴HG=GI=EF，
∴L△NEF=NE+NF+EF
=CG+CI+HG=CG+CI+DG+DH
=CG+CI+DG+BI
=（CG+DG）+（CI+BI）
=CD+BC
=2BC
=12；
∴在正方形ABCD旋转过程中，且点P在△ACD内部时，△NEF的周长不发生变化，△NEF的周长为12．

点评 此题是四边形的综合题，主要考查了正方形的性质，旋转的性质，三角形的全等的判定和性质，勾股定理，作出辅助线是本题关键，也是难点．是综合性特别强的题．