
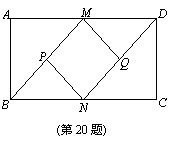
如图,在矩形ABCD中,M、N分别AD、BC的中点,P、Q分别BM、DN
的中点.
(1)求证:四边形MPNQ是菱形;
(2)若AB=2,BC=4,求四边形MPNQ的面积.
 |
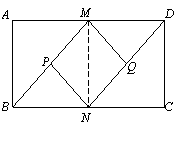
(1)证明:∵四边形ABCD是矩形,
∴AD=BC,AD∥BC.
连结MN,∵M、N分别AD、BC的中点,
 ∴MD=
∴MD=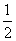 AD,BN=
AD,BN=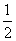 BC.
BC.
∴MD=BN,MD∥ BN,∴四边形BNDM是平行四边形.
BN,∴四边形BNDM是平行四边形.
∴MB=ND.
∵P、Q分别BM、DN的中点,∴MP=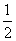 MB,NQ=
MB,NQ=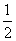 DN.
DN.
∴MP=NQ.
又∵MP∥NQ,∴四边形MPNQ是平 行四边形.
行四边形.
 ∵ABCD为矩形,M、N分别AD、BC的中点,
∵ABCD为矩形,M、N分别AD、BC的中点,
∴四边形ABNM为矩形,∴MN⊥BC.
∴在Rt△MNB中,PN=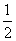 BM.∴PN=PM.
BM.∴PN=PM.
∴四边形MPNQ是菱形.
(2)∵AB=2,BC=4,∴MN=BN=2
∵P为MB的中点,∴PN⊥MB,PN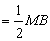
在Rt△MNB中,MB=
∴ ,∴四边形MPNQ是边长为
,∴四边形MPNQ是边长为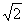 的正方形.
的正方形.
∴四边形MPNQ的面积为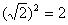


科目:初中数学 来源: 题型:
某批发商以40元/千克的成本价购入了某产品700千克,据市场预测,该产品的
销售价y(元/千克)与保存时间x(天)的函数关系为y=50+2x,但保存这批产品平均每天
将损耗15千克,且最多保存15天.另外,批发商每天保存该批产品的费用为50元.
(1)若批发商在保存该产品5天时一次性卖出,则可获利 元.
(2)如果批发商希望通过这批产品卖出获利10000元,则批发商应在保存该产品多少
天时一次性卖出?
查看答案和解析>>
科目:初中数学 来源: 题型:
反比例函数y= 和正比例函数y=mx的部分图象如图所示.
和正比例函数y=mx的部分图象如图所示.
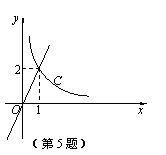 由此可以得到方程
由此可以得到方程 =mx的实数根为
=mx的实数根为
| A.x=1 | B.x=2 |
| C.x1=1,x2=-1 | D.x1=1,x2=-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
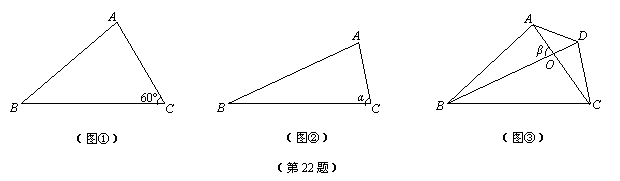
(1)如图①,若BC=6,AC=4,∠C=60°,求△ABC的面积S△ABC ;
(2)如图②,若BC=a,AC=b,∠C=α,求△ABC的面积S△ABC ;
(3)如图③,四边形ABCD,若AC=m,BD=n,对角线AC、BD交于O点,它们所成
的锐角为β.求四边形ABCD的面积S四边形ABCD .
查看答案和解析>>
科目:初中数学 来源: 题型:
某啤酒厂搞捉销活动,一箱24瓶啤酒中有4瓶的瓶盖内印有“奖”字.小明的爸爸买了
一箱这种品牌的啤酒,他连续打开了其中的4瓶均未中奖. 这时小明在剩下的啤酒中任
这时小明在剩下的啤酒中任
意打开一瓶,中奖的可能性是 ( ).
A. 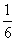 B.
B. C.
C. 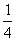 D.
D. 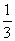
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com