练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    若a为任意实数，则下列等式中恒成立的是

    [　　]
    A．

    a＋a＝a2

    B．

    a×a＝2a

    C．3a3－2a2＝a

    D．2a×3a2＝6a3

    答案：D
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：阅读理解

    阅读理解：对于任意正实数a、b，∵(
    		a
    -
    		b
    )2    ≥0，∴a-2
    		ab
    +b    ≥0，∴a+b≥2
    		ab
    ，只有当a=b时，等号成立．
    结论：在a+b≥2
    		ab
    （a、b均为正实数）中，若ab为定值p，则a+b≥2
    		p
    ，只有当a=b时，a+b有最小值2
    		p
    ．   
    根据上述内容，回答下列问题：
    （1）若m＞0，只有当m=
     
    时，m+
    1
    m
    有最小值
     
    ；
    若m＞0，只有当m=
     
    时，2m+
    8
    m
    有最小值
     
    ．
    （2）如图，已知直线L1：y=
    1
    2
    x+1    与x轴交于点A，过点A的另一直线L2与双曲线y=
    -8
    x
    (x＞0)    相交于点B（2，m），求直线L2的解析式．
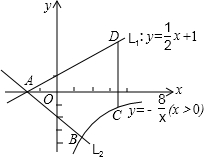    （3）在（2）的条件下，若点C为双曲线上任意一点，作CD∥y轴交直线L1于点D，试求当线段CD最短精英家教网时，点A、B、C、D围成的四边形面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    实践与探究：

    对于任意正实数a、b，∵≥0，　∴≥0，∴≥

    只有当a＝b时，等号成立。

    结论：在≥（a、b均为正实数）中，若ab为定值p，则a+b≥，只有当a＝b时，a+b有最小值。   根据上述内容，回答下列问题：

    （1）若m＞0，只有当m＝       时，有最小值         ；

    若m＞0，只有当m＝       时，2有最小值        .

    （2）如图，已知直线L1：与x轴交于点A，过点A的另一直线L2与双曲线相交于点B（2，m），求直线L2的解析式.

    （3）在（2）的条件下，若点C为双曲线上任意一点，作CD∥y轴交直线L1

    于点D，试求当线段CD最短时，点A、B、C、D围成的四边形面积.

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    实践与探究：
    对于任意正实数a、b，∵≥0，　∴≥0，∴≥
    只有当a＝b时，等号成立。
    结论：在≥（a、b均为正实数）中，若ab为定值p，则a+b≥，只有当a＝b时，a+b有最小值。  根据上述内容，回答下列问题：
    （1）若m＞0，只有当m＝      时，有最小值        ；
    若m＞0，只有当m＝      时，2有最小值       .
    （2）如图，已知直线L1：与x轴交于点A，过点A的另一直线L2与双曲线相交于点B（2，m），求直线L2的解析式.

    （3）在（2）的条件下，若点C为双曲线上任意一点，作CD∥y轴交直线L1
    于点D，试求当线段CD最短时，点A、B、C、D围成的四边形面积.

    查看答案和解析>>

    科目：初中数学 来源： 题型：阅读理解

    阅读理解：对于任意正实数a、b，∵(－)2≥0，∴a－2＋b≥0，∴a＋b≥2，只有当a＝b时，等号成立.
    结论：在a＋b≥2（a、b均为正实数）中，若ab为定值p，则a+b≥2，只有当a＝b时，a＋b有最小值2.  根据上述内容，回答下列问题：
    （1）若m＞0，只有当m＝      时，m＋有最小值        ；
    若m＞0，只有当m＝      时，2m＋有最小值       .
    （2）如图，已知直线L1：y＝x＋1与x轴交于点A，过点A的另一直线L2与双曲线y＝
    （x>0）相交于点B（2，m），求直线L2的解析式.

    （3）在（2）的条件下，若点C为双曲线上任意一点，作CD∥y轴交直线L1于点D，试
    求当线段CD最短时，点A、B、C、D围成的四边形面积.

    查看答案和解析>>

    科目：初中数学 来源：2011-2012学年江苏省江阴长泾片八年级下学期期中考试数学卷（带解析） 题型：解答题

    实践与探究：
    对于任意正实数a、b，∵≥0，　∴≥0，∴≥
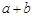    只有当a＝b时，等号成立。
    结论：在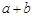≥（a、b均为正实数）中，若ab为定值p，则a+b≥，只有当a＝b时，a+b有最小值。  根据上述内容，回答下列问题：
    （1）若m＞0，只有当m＝      时，有最小值        ；
    若m＞0，只有当m＝      时，2有最小值       .
    （2）如图，已知直线L1：与x轴交于点A，过点A的另一直线L2与双曲线相交于点B（2，m），求直线L2的解析式.

    （3）在（2）的条件下，若点C为双曲线上任意一点，作CD∥y轴交直线L1
    于点D，试求当线段CD最短时，点A、B、C、D围成的四边形面积.

    查看答案和解析>>

    同步练习册答案