
【题目】抛物线![]() 上部分点的横坐标
上部分点的横坐标![]() ,纵坐标
,纵坐标![]() 的对应值如下表:
的对应值如下表:
| … |
|
|
|
|
| … |
| … |
|
|
|
|
| … |
小聪观察上表,得出下面结论:①抛物线与![]() 轴的一个交点为
轴的一个交点为![]() ;②函数
;②函数![]() 的最大值为
的最大值为![]() ;③抛物线的对称轴是
;③抛物线的对称轴是![]() ;④在对称轴左侧,
;④在对称轴左侧,![]() 随
随![]() 增大而增大.其中正确有( )
增大而增大.其中正确有( )
A. 0个 B. 1个 C. 2个 D. 3个
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD中,AB=10cm,BC=8cm,CD=12cm,∠B=∠C,点E为AB的中点.如果点P在线段BC上以3cm/s的速度沿B-C-B运动,同时,点Q在线段CD上由C点向D点运动.当点Q的运动速度为_______cm/s时,能够使△BPE≌△CQP.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
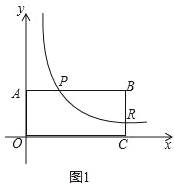
反比例函数y=![]() (k>0)第一象限内的图象如图1所示,点P、R是双曲线上不同的两点,过点P、R分别做PA⊥y轴于点A,RC⊥x轴于点C,两垂线交点为B.
(k>0)第一象限内的图象如图1所示,点P、R是双曲线上不同的两点,过点P、R分别做PA⊥y轴于点A,RC⊥x轴于点C,两垂线交点为B.
(1)问题提出:线段PB:PA与BR:RC有怎样的关系?
问题解决:设点PA=n,PB=m,则点P的坐标为(n,![]() ),点R的坐标为(m+n,
),点R的坐标为(m+n,![]() ),AO=BC=
),AO=BC=![]() ,RC=
,RC=![]() ,BR=
,BR=![]()
![]() =
=![]()
则BR:RC=![]()
![]() ,
,
PB:PA=![]()
∴PB:PA=BR:RC.
问题应用:
(2)利用上面的结论解决问题:
①如图1,如果BR=6,CR=3,AP=4,BP=_____.
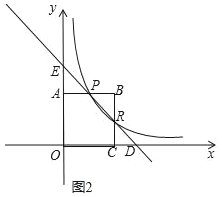
②如图2,如果直线PR的关系式y2=﹣x+3,与x轴交于点D,与y轴交于点E,若ED=3PR,求出k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近几年来,为了缓减环境污染,某区加大了对煤改电的投资力度,该区居民在2015年有7500户完成煤改电,2017年有10800户完成了煤改电.
(1)求该区2015年至2017年完成煤改电户数的年平均增长率;
(2)2018年该区计划要完成煤改电的户数比2017年要有所增长,但增长率不超过15%,请求出2018年最多有多少户能完成煤改电.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=nx2﹣3nx﹣4n(n<0)与x轴交于B、C两点(点B在点C的左侧),且抛物线与y轴交于点A.
(1)点B的坐标为 ,点C的坐标为 ;
(2)若∠BAC=90°,求抛物线的解析式.
(3)点M是(2)中抛物线上的动点,点N是其对称轴上的动点,是否存在这样的点M、N,使得以A、C、M、N为顶点的四边形是平行四边形?若存在,请直接写出点M的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 与
与![]() 轴交点的横坐标为
轴交点的横坐标为![]() ,
,![]() ,则对于下列结论:
,则对于下列结论:
①当![]() 时,
时,![]() ;
;
②方程![]() 有两个不相等的实数根
有两个不相等的实数根![]() ,
,![]() ;
;
③![]() .
.
其中正确的结论有________(只需填写序号即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=2点,D是AC中点,将△ABD沿BD所在直线折叠,使点A落在点P处,连接PC.
(1)写出BP,BD的长;
(2)求证:四边形BCPD是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)
如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.

(1)求证:AB=DC;
(2)试判断△OEF的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com