解:(1)∵OC=4,
∴点C的坐标为(0,4).
∴c=4,则抛物线解析式为y=ax
2+bx+4.
∵AO=2OC,则AO=8,
∴点A的坐标为(-8,0).
又∵抛物线对称轴为直线x=-3,
∴点B的坐标为(2,O).
∴
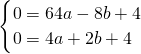
,
解得
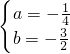
.
∴该抛物线的函数表达式为

.
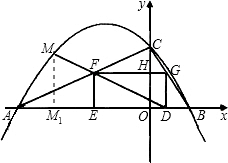
(2)∵矩形DEFG中FG∥ED,设FG与y轴交于点H,
∴△CFH∽△CAO,△CHG∽△COB.
∴
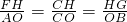
,即
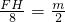
.
∴FH=4m,故FG=5m.
设直线BC的解析式为:y=kx+b
1,则
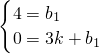
,
解得
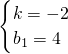
.
∴直线BC的解析式为y=-2x+4,则点G的坐标为(m,-2m+4)
∴S=FG×GD=5m(-2m+4)=-10(m-1)
2+10
∵0≤m≤2,
∴当m=1时,S最大.此时OD=1,OE=4,∴DE=5.
过M作MM
1⊥x轴于M
1,则△MM
1D∽△FED,
∴
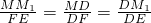
∵
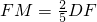
,
∴
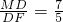
.则
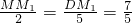
.
∴

,DM
1=7,则OM
1=6.
∴此时点M的坐标为
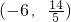
.
(3)存在.理由如下:
∵点Q在抛物线上,且横坐标为-4,
∴y
Q=6,
∴点Q坐标为(-4,6),
设P的坐标为(0,n),在△BPQ中,
若∠BQP为直角,则PQ
2+BQ
2=BP
2,
∴4
2+(n-6)
2+6
2+(2+4)
2=2
2+n
2,
解得n=10,
此时点P的坐标为(0,10).
若∠QBP为直角,则PQ
2=BQ
2+BP
2,
∴4
2+(6-n)
2=6
2+(2+4)
2+2
2+n
2,
解得n=-2,
此时点P的坐标为(0,-2).
若∠QPB为直角,则BQ
2=BP
2+PQ
2,
∴6
2+(2+4)
2=4
2+(n-6)
2+2
2+n
2,
解得
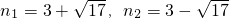
此时点P的坐标为
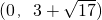
或
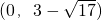
.
综上所述,存在这样的点P,使得以△BPQ是直角三角形,所求的点P的坐标为:
(O,10)或(0,-2)或
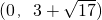
或
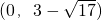
.
分析:(1)求出点C的坐标,则得出c=4.根据抛物线的性质求出点A,B的坐标.然后把已知坐标代入解析式求出函数表达式.
(2)证明△CFH∽△CAO,△CHG∽△COB利用线段比求出FH,FG.然后设直线BC的解析为y=kx+b
1,求出解析式后可求出点G的坐标为(m,-2m+4),然后可求出S的函数解析式.做MN
1⊥x轴于M
1,证明△MM
1D∽△FED,利用线段比有关线段的值最后求出点M的坐标.
(3)依题意求出点Q的坐标,设P点坐标为(0,n).在△BPQ中,分三种情况讨论点P的坐标.
点评:本题考查的是二次函数的综合运用.利用待定系数法以及结合二次函数图象求解,难度较大.

 抛物线对称轴为直线x=-3.
抛物线对称轴为直线x=-3.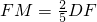 ,求出此时点M的坐标;
,求出此时点M的坐标; 解:(1)∵OC=4,
解:(1)∵OC=4,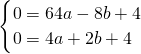 ,
,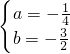 .
. .
.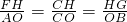 ,即
,即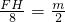 .
.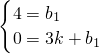 ,
,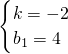 .
.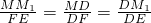
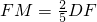 ,
,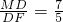 .则
.则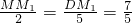 .
. ,DM1=7,则OM1=6.
,DM1=7,则OM1=6.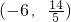 .
.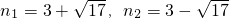
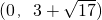 或
或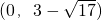 .
.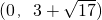 或
或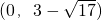 .
.

 两点,试问当x为何值时,线段CD有最大值,其最大值为多少?
两点,试问当x为何值时,线段CD有最大值,其最大值为多少? O为坐标原点,抛物线上一点C的横坐标为1.
O为坐标原点,抛物线上一点C的横坐标为1. 此抛物线上,矩形面积为12,
此抛物线上,矩形面积为12, 与x轴交于点A、B,点A的坐标为(-2,0).
与x轴交于点A、B,点A的坐标为(-2,0).